SCPS145B December 2007 – February 2016 P82B715
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Pin Configuration and Functions
- 6 Specifications
- 7 Parameter Measurement Information
- 8 Detailed Description
- 9 Application and Implementation
- 10Power Supply Recommendations
- 11Layout
- 12Device and Documentation Support
- 13Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9 Application and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
9.1 Application Information
The P82B715 can operate with a supply voltage from 3 V to 12 V, but the logic-signal levels at Sx/Lx are independent of the supply voltage. They remain at the levels presented to the chip by the attached devices. The maximum static I2C bus sink current, 3 mA, flowing in either direction in the internal current sense resistor, causes a difference less than 100 mV in the bus logic low levels at Sx and Lx. This makes P82B715 fully compatible with all logic signal drivers, including TTL. The P82B715 cannot modify the bus logic signal voltage levels, but it contains internal diodes connected between Lx/Sx and VCC that conduct and limit the logic signal swing if the applied logic levels would have exceeded the supply voltage by more than 0.7 V.
In normal applications, external pullup resistors pull the connected buses up to the desired voltage high level. Usually this is the supply voltage, VCC, but for very low logic voltages, it is necessary to use a VCC of at least 3.3 V and preferably higher. Note that full performance over temperature is ensured only from 4.5 V. Specification deratings apply when its supply voltage is reduced below 4.5 V. The absolute minimum VCC is 3 V.
9.2 Typical Application
By using two (or more) P82B715 devices, a subsystem can be built that retains the interface characteristics of a normal I2C device so that the subsystem may be included in, or added to, any I2C or related system.
The subsystem features a low-impedance or buffered bus capable of driving large wiring capacitance (see Figure 4).
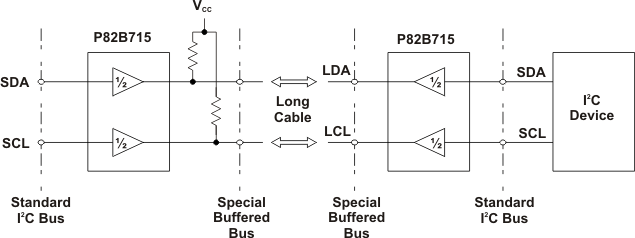 Figure 4. Minimum Subsystem Diagram
Figure 4. Minimum Subsystem Diagram
9.2.1 Design Requirements
Table 1 lists the design parameters for this example.
Table 1. Design Parameters
| PARAMETER | DESCRIPTION | VALUE |
|---|---|---|
| VCC | Supply Voltage | 3.3 V |
| CLx | Capacitance on the Lx / Ly bus | 3000 pF |
| RPU_Sx | Pullup resistor for the Sx / Sy bus | 4700 Ω |
| RPU_Lx | Pullup resistor for the Lx / Ly bus | 330 Ω |
9.2.2 Detailed Design Procedure
9.2.2.1 I2C Systems
As in standard I2C systems, pullup resistors are required to provide the logic high levels on the buffered bus, as the standard open-collector configuration is retained. The size and number of pullup resistors depends on the system.
If P82B715 devices are to be permanently connected into a system, the circuit may be configured with only one pullup resistor on the buffered bus and none on the I2C buses, but the system design is simplified, and performance is improved by fitting separate pullups on each section of the bus. When a subsystem using P82B715 may be optionally connected to an existing I2C system that already has a pullup, the effects of the subsystem pullups acting in parallel with the existing I2C bus pullup must be considered.
9.2.2.2 Pullup Resistance Calculation
When calculating the pullup resistance values, the gain of the buffer introduces scaling factors that must be applied to the system components. In practical systems, the pullup resistance value is calculated to meet the rise time limit for I2C systems. As an approximation, this limit is satisfied in a 100-kHz system if the time constant of the total system (product of the net resistance and net capacitance) is set to 1 μs or less.
In systems using the P82B715, it is convenient to set the total system time constant by considering each bus node separately (that is, the I2C nodes and the buffered bus node) and selecting a separate pullup resistor for each node to provide time constants of less than 1 μs. If each node complies then the system requirement is also met.
This arrangement, using multiple pullups as shown in Figure 5, provides the best system performance and allows stand-alone operation of individual I2C buses if parts of the extended system are disconnected or reconnected. For each bus section, the pullup resistor is calculated as:
where
- Cdevice = Sum of any connected device capacitances
- Cwiring = Total wiring and stray capacitance on the bus section
The 1 μs is an approximation with a safety factor to the theoretical time constant necessary to meet the specified 1-μs bus rise-time specification in a system with variable logic thresholds, where the CMOS limits of 30% and 70% of VCC apply. The calculated value is 1.18 μs.
If these capacitances cannot be measured or calculated, an approximation can be made by assuming that each device presents 10 pF of load capacitance and 10 pF of trace capacitance, and that cables range from 50 pF to 100 pF per meter.
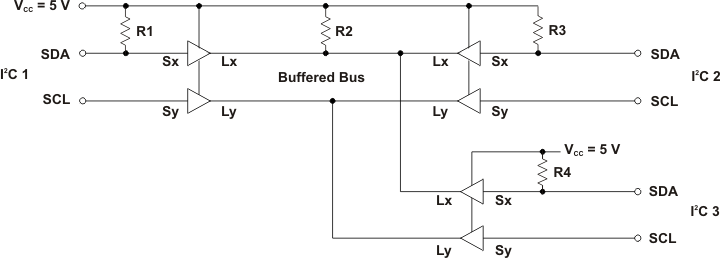 Figure 5. Single Pullup Buffered Bus
Figure 5. Single Pullup Buffered Bus
If only a single pullup is used, it must be placed on the buffered bus (as R2 in Figure 5) and the associated total system capacitance calculated by combining the individual bus capacitances into an equivalent capacitive loading on the buffered bus.
This equivalent capacitance is the sum of the capacitance on the buffered bus plus ten times the sum of the capacitances on all the connected I2C nodes. The calculated value should not exceed 4 nF. The single buffered bus pullup resistor is then calculated to achieve the 1-μs rise time, and it provides the pullup for the buffered bus and for all other connected I2C bus nodes included in the calculation.
9.2.2.3 Calculating Bus Drive Currents
Figure 5 shows three P82B715 devices connected to a common buffered bus. The associated bus capacitances are omitted for clarity, but assume the resistors have been selected to give R-C products of less than 1 μs so the bus rise-time requirement is satisfied. An I2C device connected at I2C 1 and holding the SDA bus low must sink the current flowing in its local pullup R1, plus, with assistance from the P82B715, the currents in R2, R3, and R4. Because the resistors R3 and R4 act to pull the bus nodes I2C 2 and I2C 3 and their corresponding Sx pins to a voltage higher than the voltage at the Lx pins, their buffer amplifiers are inactive. The SDA at Sx of I2C 2 and I2C 3 is pulled low by the low at Lx through the internal 30-Ω resistor that links Lx to Sx. So the effective current that must be sunk by the P82B715 buffer on I2C 1 at its Lx pin is the sum of the currents in R2, R3, and R4. The Sx current that must be sunk by an I2C device at I2C 1 due to the buffer gain action is 1/10 of the Lx current. So the effective pullup determining the current to be sunk by an I2C device at I2C 1 is R1 in parallel with resistors ten times the values of R2, R3, and R4. If R1 = R3 = R4 = 10 kΩ, and R2 = 1 kΩ, the effective pullup load at I2C 1 is 10 kΩ||10 kΩ||100 kΩ||100 kΩ = 4.55 kΩ.
The same calculation applies for I2C 2 or I2C 3.
To calculate the current sunk by the Lx pin of the buffer at I2C 1, note that the current in R1 is sunk directly by the device at I2C 1. The buffer, therefore, sinks only the currents flowing in R2, R3, and R4, so the effective pullup is R2 in parallel with R3 and R4.
In this example that is 1 kΩ||10 kΩ||10 kΩ = 833 Ω. For a 5.5-V supply and 0.4-V low, the buffer is sinking 16.3 mA.
The P82B715 has a static sink rating of 30 mA at Lx. The requirement is that the pullup on the buffered bus, in parallel with all other pullups that it is indirectly pulling low on Sx pins of other P82B715 devices, does not cause this 30-mA limit to be exceeded.
The minimum pullup resistance in a 5-V ± 10% system is 170 Ω.
The general requirement is:
where
- Rp = Parallel combination of all pullup resistors driven by the Lx pin of the P82B715
Figure 6 shows calculations for an expanded I2C bus with 3 nF of cable capacitance.
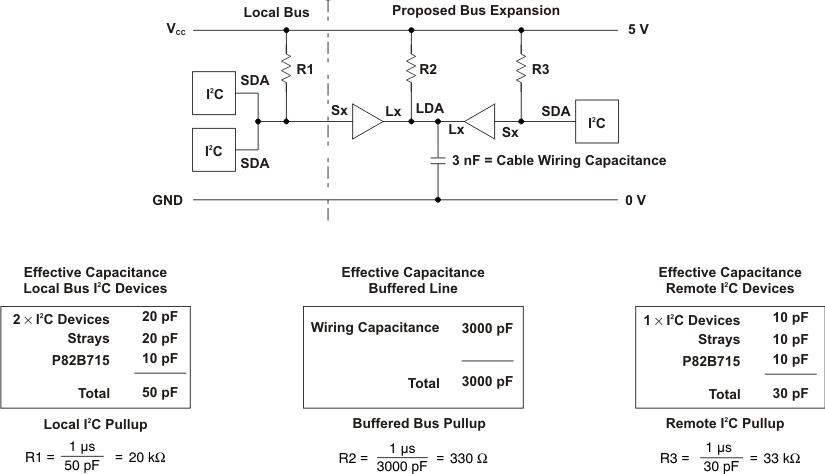 Figure 6. Typical Loading Calculations
Figure 6. Typical Loading Calculations
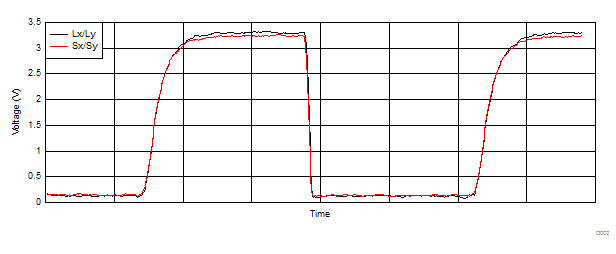
9.2.3 Application Curve