SNAS714C November   2016  – August 2021 LMS3635-Q1 , LMS3655-Q1

PRODUCTION DATA  

  1. 1 Features
  2. 2 Applications
  3. 3 Description
  4. 4 Revision History
  5. 5 Device Comparison Tables
  6. 6 Pin Configuration and Functions
  7. 7 Specifications
    1. 7.1 Absolute Maximum Ratings
    2. 7.2 ESD Ratings
    3. 7.3 Recommended Operating Conditions
    4. 7.4 Thermal Information
    5. 7.5 Thermal Information (for Device Mounted on PCB)
    6. 7.6 Electrical Characteristics
    7. 7.7 System Characteristics
    8. 7.8 Timing Requirements
    9. 7.9 Typical Characteristics
  8. 8 Detailed Description
    1. 8.1 Overview
    2. 8.2 Functional Block Diagram
      1. 8.2.1 Control Scheme
    3. 8.3 Feature Description
      1. 8.3.1 RESET Flag Output
      2. 8.3.2 Enable and Start-Up
      3. 8.3.3 Soft-Start Function
      4. 8.3.4 Current Limit
      5. 8.3.5 Hiccup Mode
      6. 8.3.6 Synchronizing Input
      7. 8.3.7 Undervoltage Lockout (UVLO) and Thermal Shutdown (TSD)
      8. 8.3.8 Input Supply Current
    4. 8.4 Device Functional Modes
      1. 8.4.1 AUTO Mode
      2. 8.4.2 FPWM Mode
      3. 8.4.3 Dropout
      4. 8.4.4 Spread-Spectrum Operation
  9. 9 Application and Implementation
    1. 9.1 Application Information
    2. 9.2 Typical Applications
      1. 9.2.1 General Application
        1. 9.2.1.1 Design Requirements
        2. 9.2.1.2 Detailed Design Procedure
          1. 9.2.1.2.1 Custom Design With WEBENCH® Tools
          2. 9.2.1.2.2 External Components Selection
            1. 9.2.1.2.2.1 Input Capacitors
            2. 9.2.1.2.2.2 Output Inductors and Capacitors
              1. 9.2.1.2.2.2.1 Inductor Selection
              2. 9.2.1.2.2.2.2 Output Capacitor Selection
          3. 9.2.1.2.3 Setting the Output Voltage
          4. 9.2.1.2.4 FB for Adjustable Output
          5. 9.2.1.2.5 VCC
          6. 9.2.1.2.6 BIAS
          7. 9.2.1.2.7 CBOOT
          8. 9.2.1.2.8 Maximum Ambient Temperature
        3. 9.2.1.3 Application Curves
      2. 9.2.2 Fixed 5-V Output for USB-Type Applications
        1. 9.2.2.1 Design Requirements
        2. 9.2.2.2 Detailed Design Procedure
        3. 9.2.2.3 Application Curves
      3. 9.2.3 Fixed 3.3-V Output
        1. 9.2.3.1 Design Requirements
        2. 9.2.3.2 Detailed Design Procedure
        3. 9.2.3.3 Application Curves
      4. 9.2.4 6-V Adjustable Output
        1. 9.2.4.1 Design Requirements
        2. 9.2.4.2 Detailed Design Procedure
        3. 9.2.4.3 Application Curves
    3. 9.3 Do's and Don't's
  10. 10Power Supply Recommendations
  11. 11Layout
    1. 11.1 Layout Guidelines
    2. 11.2 Layout Example
  12. 12Device and Documentation Support
    1. 12.1 Device Support
      1. 12.1.1 Third-Party Products Disclaimer
      2. 12.1.2 Development Support
        1. 12.1.2.1 Custom Design With WEBENCH® Tools
    2. 12.2 Documentation Support
      1. 12.2.1 Related Documentation
    3. 12.3 Receiving Notification of Documentation Updates
    4. 12.4 Support Resources
    5. 12.5 Trademarks
    6. 12.6 Electrostatic Discharge Caution
    7. 12.7 Glossary
  13. 13Mechanical, Packaging, and Orderable Information

Package Options

Mechanical Data (Package|Pins)
Thermal pad, mechanical data (Package|Pins)
Orderable Information

8.4.1 AUTO Mode

In AUTO mode the device moves between PWM and PFM as the load changes. At light loads, the regulator operates in PFM. At higher loads, the mode changes to PWM. The load currents at which the mode changes can be found in the Section 9.2.2.3.

In PWM, the converter operates as a constant frequency, current mode, full synchronous converter using PWM to regulate the output voltage. While operating in this mode the output voltage is regulated by switching at a constant frequency and modulating the duty cycle to control the power to the load. This provides excellent line and load regulation and low output voltage ripple. When in PWM, the converter synchronizes to any valid clock signal on the SYNC input (see Section 8.3.6); during PFM operation, the SYNC input is ignored.

In PFM, the high-side FET is turned on in a burst of one or more cycles to provide energy to the load. The frequency of these bursts is adjusted to regulate the output, while diode emulation is used to maximize efficiency (see the Glossary). This mode provides high light-load efficiency by reducing the amount of input supply current required to regulate the output voltage at small loads. A small increase in the output voltage occurs in PFM. This trades off very good light load efficiency for larger output voltage ripple and variable switching frequency. The actual switching frequency and output voltage ripple depend on the input voltage, output voltage, and load. See the Section 9.2.2.3 for output voltage variation in AUTO mode. A typical switching waveform for PFM is shown in Figure 8-7.

A unique feature of this device is that a minimum input voltage is required for the regulator to switch from PWM to PFM at light load. This feature is a consequence of the advanced architecture employed to provide high efficiency at light loads. Figure 8-8 indicates typical values of input voltage required to switch modes at no load. Also, once the regulator switches to PFM at light load, it remains in that mode if the input voltage is reduced.

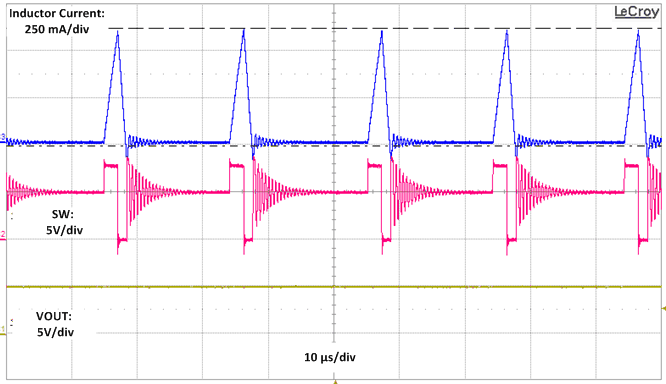GUID-1331B8AF-8C71-410B-9AC6-0CB449AA13FC-low.gifFigure 8-7 Typical PFM Switching Waveforms
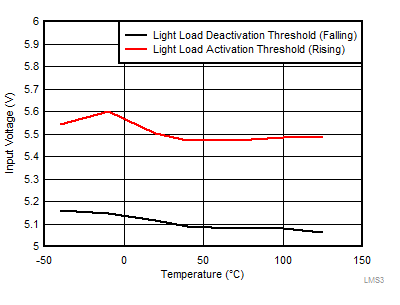GUID-FF9A46DA-7376-46AD-B023-30DD0595070B-low.gifFigure 8-9 Input Voltage for Mode Change — 5-V Output, 10-µH Inductor
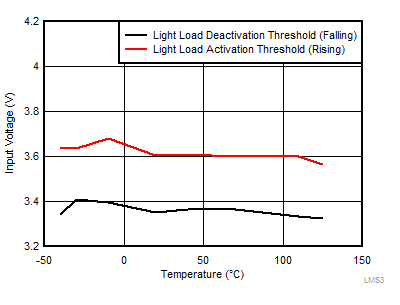GUID-47BF20B6-CB8A-4892-9C7C-198A6BE9D040-low.gifFigure 8-8 Input Voltage for Mode Change — 3.3-V Output, 10-µH Inductor