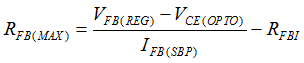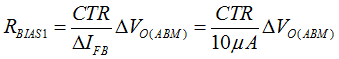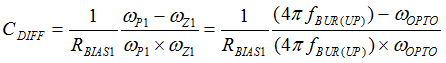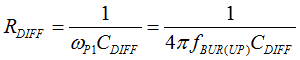SLUSD12A October 2017 – February 2018 UCC28780
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Pin Configuration and Functions
- 6 Specifications
-
7 Detailed Description
- 7.1 Overview
- 7.2 Functional Block Diagram
- 7.3
Detailed Pin Description
- 7.3.1 BUR Pin (Programmable Burst Mode)
- 7.3.2 FB Pin (Feedback Pin)
- 7.3.3 VDD Pin (Device Bias Supply)
- 7.3.4 REF Pin (Internal 5-V Bias)
- 7.3.5 HVG and SWS Pins
- 7.3.6 RTZ Pin (Sets Delay for Transition Time to Zero)
- 7.3.7 RDM Pin (Sets Synthesized Demagnetization Time for ZVS Tuning)
- 7.3.8 RUN Pin (Driver Enable Pin)
- 7.3.9 SET Pin
- 7.4
Device Functional Modes
- 7.4.1 Adaptive ZVS Control with Auto-Tuning
- 7.4.2 Dead-Time Optimization
- 7.4.3 Control Law across Entire Load Range
- 7.4.4 Adaptive Amplitude Modulation (AAM)
- 7.4.5 Adaptive Burst Mode (ABM)
- 7.4.6 Low Power Mode (LPM)
- 7.4.7 Standby Power Mode (SBP)
- 7.4.8 Startup Sequence
- 7.4.9 Survival Mode of VDD
- 7.4.10 System Fault Protections
- 7.4.11 Pin Open/Short Protections
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Application Circuit
- 8.2.1 Design Requirements
- 8.2.2 Detailed Design Procedure
- 8.2.3 Application Curves
- 9 Power Supply Recommendations
- 10Layout
- 11Device and Documentation Support
- 12Mechanical, Packaging, and Orderable Information
Package Options
Refer to the PDF data sheet for device specific package drawings
Mechanical Data (Package|Pins)
- D|16
- RTE|16
Thermal pad, mechanical data (Package|Pins)
- RTE|16
Orderable Information
8.2.2.7 Calculation of Compensation Network
UCC28780 integrates two control concepts to benefit high-efficiency operation: peak current-mode control and burst ripple control. The peak current loop in AAM can be analyzed based on the linear control theory, so the compensation target is to obtain enough phase margin and gain margin for the given small-signal characteristic of an active clamp flyback converter. For transition-mode operation, the power stage can be modeled as a voltage-controlled current source charging an output capacitor (CO) with an equivalent-series resistance (RCo) and the output load (RO) as shown in Figure 37. The first-order plant characteristic and high switching frequency operation in AAM make the peak current loop easier to stabilize than ABM.
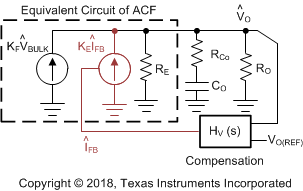 Figure 37. Small-Signal Model of ACF in AAM Loop
Figure 37. Small-Signal Model of ACF in AAM LoopThe adaptive burst mode (ABM) is a ripple-based control, so the linear control theory for AAM cannot be applied. The most critical stability criterion of burst control is to make the burst ripple content of IFB to be in-phase with the burst ripple voltage of VO. In normal operation, the fundamental burst frequency (fBUR) in ABM varies between 20 kHz and 40 kHz. An example of normal burst operation is illustrated in Figure 38.
 Figure 38. Expected Burst Pattern Example
Figure 38. Expected Burst Pattern ExampleStrong phase-delay in the frequency range creates slope distortion around the intersection point between IFB and ITH(FB), so the ripple regulator generates inconsistent burst off-times. As shown in Figure 39, the sub-harmonic oscillation at half of fBUR is a typical phenomenon of an unstable ABM loop. Two burst packets are adjacent to each other and the pulse count (NSW) is different by one pulse count.
 Figure 39. Typical Behavior of Unstable ABM Loop
Figure 39. Typical Behavior of Unstable ABM Loop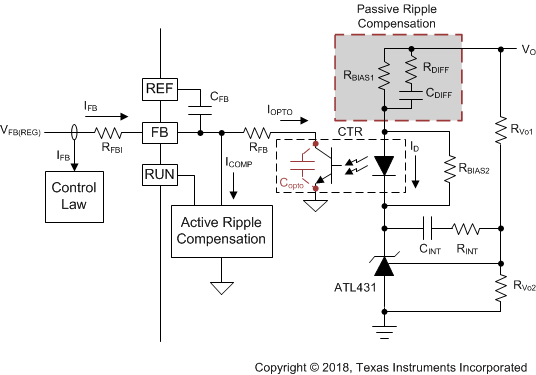 Figure 40. Compensation Network, Hv(s)
Figure 40. Compensation Network, Hv(s)In order to minimize the phase-delay of IFB, the transfer function from IFB to VO guides the pole/zero placement of the secondary-side passive ripple compensation network in Figure 40. In the primary-side control circuitry, two poles at ωFB and ωOPTO introduce phase-delay on IFB. ωFB pole is formed by the external filter capacitor CFB and the parallel resistance of the internal RFBI and the external current-limiting resistor (RFB). ωOPTO pole is formed by the parasitic capacitance of the optocoupler output (COPTO) and the series resistance of RFBI and RFB. For CFB = 100 pF, RFBI = 8 KΩ, and RFB = 20 KΩ, the delay effect of ωFB pole located at 278 kHz is negligible. However, ωOPTO pole is located less than 10 kHz, and introduces large phase delay in the interested fBUR range of ABM, since COPTO is in a few nF range contributed by the Miller effect of the collector-to-base capacitance of the BJT in the optocoupler output. Therefore, an RC network (RDIFF and CDIFF) in parallel with RBIAS1 is used to compensate the phase-delay of the optocoupler, which introduces an extra pole/zero pair located at ωP1 and ωZ1 respectively. The basic design guide is to place the ωZ1 zero close to the ωOPTO pole, and to place ωP1 pole away from highest fBUR.
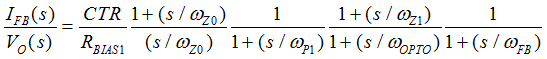
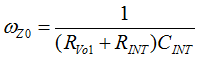
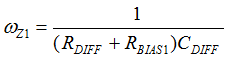
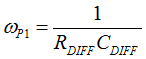
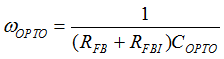
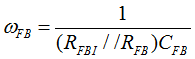
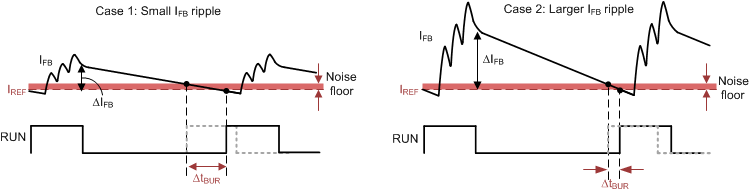 Figure 41. Effect of Signal-to-Noise Ratio of iFB to ABM Operation
Figure 41. Effect of Signal-to-Noise Ratio of iFB to ABM Operation Another guideline of obtaining a more consistent burst off-time is to maintain large enough ripple amplitude of IFB in ABM mode (ΔIFB) for better signal-to-noise ratio. Figure 41 shows that when the noise floor alters the intersection point of each burst cycle, larger ΔIFB performs much less burst off-time variation if the noise floor stays the same. ΔIFB around 10 μA is a recommended initial design value. The ripple ratio (KRIPPLE) between ΔIFB and the burst voltage ripple of VO in ABM (ΔVO(ABM)) is obtained by simplifying the small-signal gain of IFB(s)/VO(s) transfer function between 20 kHz and 40 kHz.
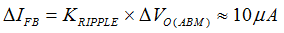
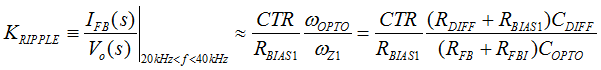
With the above understanding on burst control, the step-by-step design procedure is:
- RFB selection needs to consider both the output voltage regulation and compensation challenge on the low-frequency pole at ωOPTO. RFB should be less than the maximum value of 28 kΩ to provide a sufficient feedback current of 95 μA for the output voltage regulation in SBP mode, under the worst-case VFB(REG) and RFBI. RFB = 28 kΩ and COPTO = 2 nF result in the ωOPTO pole located at 2.8 kHz. Such a low-frequency pole forces the ωZ1 zero to be designed around 2.8 kHz to compensate the phase-delay.
- RBIAS1 is determined based on a given current transfer ratio (CTR) of the optocoupler, ΔVO(ABM), and target 10 μA of ΔIFB as example.
- CDIFF is designed to position ωZ1 ≈ ωOPTO and locate ωP1 at least two-times higher frequency than 2π x fBUR(UP) as example.
- RDIFF is designed to position ωP1 two-times higher than 2π x fBUR(UP), but lower than the switching frequency in ABM (2π x fSW(BUR)). Too small of RDIFF moves ωP1 higher than 2π x fSW(BUR), so the high differentiation gain on the secondary-side compensator amplifies the switching ripple and increases the noise floor. Therefore, RDIFF should be fine-tuned based on the actual noise level of a given design.
- RINT selection is not designed for the small-signal compensation, but to resolve the slow large-signal response of the shunt regulator. Specifically, after a step-down load change from heavy load to no load occurs, the output voltage overshoot and the long settling time forces ATL431 to reduce the cathode voltage continuously by the integrator configuration of ATL431 until the output voltage gets back to normal regulation level. If the load step-up transient happens before the output voltage is settled from the previous load step-down event, the low voltage across ATL431 becomes the initial voltage level for the integrator to move to a new steady-state. Since the time for ATL431 moving from lower voltage to a high voltage delays iFB reduction, the controller response from SBP mode to AAM mode is delayed as well, which slows down the energy delivery to the output and results in a large voltage undershoot. To resolve this problem, RINT behaves like a current-limiting resistor for CINT, which slows down the reduction on the cathode voltage of ATL431. RINT needs to be adjusted based on the voltage undershoot requirement under the lowest repetitive rate of load change.