Design Steps

See the Design References section for an Excel calculator that calculates the resistor values for the required specifications.

1. Define the input voltage range for the circuit. For this design V_{in_min} = 0 V, V_{in_max} = 5 V is chosen.
2. Define the output current range for the circuit. For this design I_{out_min} = 4 mA, I_{out_max} = 20 mA is selected.
3. Calculate R₇ and R₈ to set the output voltage for the TPS7A4501-SP LDO. The equation to set the output voltage for this adjustable LDO follows:
   

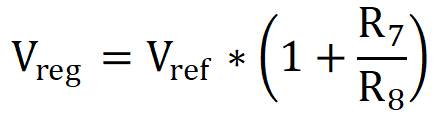
   In this equation, V_ref is the internal bandgap reference voltage for the LDO. TPS7A4501-SP has a nominal reference voltage V_ref = 1.21 V and this design is targeting V_reg = 5 V, so the following applies:

   
   

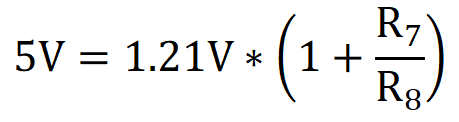
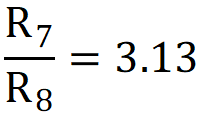
   To choose values, the following guideline is used: The current in the feedback resistors from output to ground of an LDO must be at least 100 times the leakage current into the ADJ pin to avoid output accuracy issues. For TPS7A4501-SP, the leakage current of the ADJ pin is 3 μA (typ). This yields the following inequality:

   
   
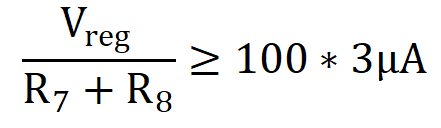
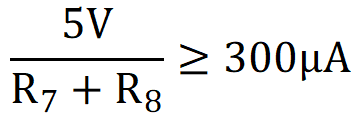   16.67 kΩ ≥ R₇ + R₈

   With R₈ = 3.97 kΩ (standard value), the following equation is true:

   R₇ = 3.97 kΩ * 3.13 = 12,426 Ω ≈ 12.4 kΩ (standard value)

   With these values for R₇ and R₈, the following equation is valid:

   R₇ + R₈ = 3.97 kΩ + 12.4 kΩ = 16.37 kΩ ≤ 16.67 kΩ
   Note: Since this design has a current budget limitation, it is desirable to size R₇ and R₈ to be near the limit to minimize this quiescent current contribution.
   
   
4. Define the minimum and maximum currents through R₃. See Design Note #5 before defining these currents. For this design, I_{3_min} = 20 μA, I_{3_max} = 100 μA, is chosen.
5. Calculate the values for R₁ and R₂ to set I_{3_min} and I_{3_max} as defined in Design Step #4. To do this, use the first equation along with the specifications for V_reg, V_{in_min}, V_{in_max}, I_{3_min} and I_{3_max}. When V_in = V_{in_min}, the following equations occur:
   
   
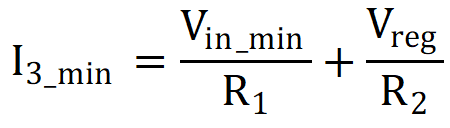
   R₂ = 250 kΩ (standard value)

   When V_in = V_{in_max}, the following is true:

   
   
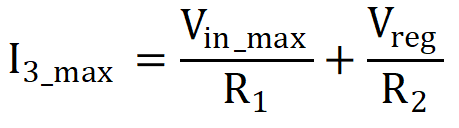
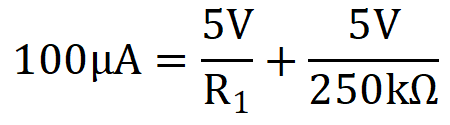   R₁ = 62.5 kΩ ≈ 62 kΩ (standard value)
6. Calculate R₃ / R₄ to set the required current gain. To do this, use this equation along with I_{out_min} and I_{3_min}.
   
   
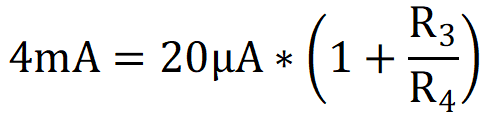
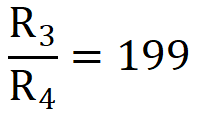   Note: Only the minimum values of I_out and I₃ are required to calculate R₃ / R₄ because it is assumed that Design Note #5 has been followed.
   
   
7. Choose values for R₃ and R₄. Sizing R₃ is much less important than sizing R₄ because headroom issues can arise if care is not taken when sizing R₃. To see why, analyze the nodal voltages under the maximum loading condition, I_out = I_{out_max} = 20 mA. The load voltage is the following:
   V_load = I_{out_max} * R_load = 20 mA × 250 Ω = 5 V

   Most of the output current comes through R₄, so with R₄ = 100 Ω, the voltage at I_ret is approximately:

   5 V + 100 Ω * 20 mA = 7 V

   V_reg is referenced to I_ret, so relative to the supply ground, V_reg = 7 V + 5 V = 12 V, in which case the LDO enters dropout. If the LDO enters dropout, the LDO loses its power supply rejection (PSR) properties, and the op amp has a reduced positive supply and so has a reduced ability to drive the base of the transistor to provide additional output current. Furthermore, if V_reg droops, the current through R₃ will be reduced and the circuit begins to exhibit non-linear behavior. Also, if R₆ is too large, the additional voltage drop across R₆ further reduces the available headroom for the transistor.

   With these considerations in mind, choose R₄ = 50 Ω to avoid problems with headroom. It follows that:

   R₃ = 199 * 50 Ω = 9.95 kΩ ≈ 9.88 kΩ (standard value)