Design Steps

Component Selection

1. Identify the current sink specifications:
   • Specifications for the circuit shown:
     • Input voltage range (DAC output): 0mV to 500mV
     • Resistive load: 15Ω
     • Load current range: 0mA to 200mA
     • Current error: ±4mA
2. Sense resistor selection (R_Sense):
   • The selection of R_Sense comes down to power dissipation versus precision.
     • Smaller values of R_Sense yield smaller voltage drops for the same amount of current and ultimately dissipate less power. However, since the R_Sense voltage drop is smaller, higher precision components may need to be used to achieve the same error tolerance.
     • Higher values of R_Sense can be created by paralleling resistors to share the power dissipation.
   • In the circuit shown, the R_Sense value is selected based on the maximum DAC output voltage (V_DACMax) and the maximum load current (I_Max) as shown:
     $R_{Sense}=\frac{V_{DACMax}}{I_{Max}}$
     $R_{Sense}=2.5\Omega =\frac{500mV}{200mA}$
   • In this case, the 2.5-Ω R_Sense produces a voltage of 10mV per 4mA of load current. Therefore, to meet the desired current error specification of ±4mA, the total voltage error should be less than 10mV (2.5Ω × 4mA). The total voltage error includes the offset voltage error from the op amp, the op amp input bias current error through resistor RF, DAC output error, and the R_Sense resistor error.
     • Fortunately, the LMP7704-SP has great DC performance with a typical offset voltage of ±32µV and a typical input bias current of ±0.2pA. Calculate the error contribution as follows:
       $Error \left(mV\right)=\left(\left(Vos\right)+\left(\left(IB\right)\times RF\right)\right)\times 1000$
       $Error \left(mV\right)=0.032mV=\left(\left(\pm 32uV\right)+\left(\left(\pm 0.2pA\right)\times 1\mathrm{k\Omega }\right)\right)\times 1000$
     • The DC error of the amplifier, as shown, is not a significant contributor to the allowed 10mV of error.
     • In many cases, most of the error is observed from the R_Sense tolerance, R_Sense drift, and the DACs offset error, gain error, and drift.
     • Use the DAC121S101QML-SP to achieve the circuit requirements and maintain the radiation performance.
3. Amplifier selection (U1A):
   • The amplifier selection is rather straightforward. From the perspective of meeting the current error specifications, consider the offset voltage of the op amp and its input bias current (as shown previously in the Sense Resistor Selection section).
   • The op amp should also have an input common-mode range that extends to the negative rail (GND in this case) to support the low output range of the DAC. However, there is a hidden criterion for selection under one or both of the following two conditions: (1) the MOSFET has a threshold voltage (V_GS(th)) close to the available supply rail, (2) the resistive load of the system is close to the maximum load the supply rail can handle.
   • The hidden criterion is the output voltage swing of the op amp. Looking the circuit, the selected MOSFET Q1 has a maximum V_GS(th) across TID exposure of 4V and the circuit supply rail is 5V. At peak current, the source voltage of the MOSFET is at 0.5V which is also the voltage across R_Sense (200mA × 2.5Ω). In this case, the op amp with the 5-V supply must be able to swing to at least (V+) – 0.5V or 4.5V to reach V_GS(th). Similarly, in the case of condition (2) the op amp must be able to swing close to the positive rail to maximize the largest resistive load that can be driven.
   • Calculate the largest resistive load as follows (assuming no voltage drop across Q1):
     $R_{LoadMax}=\frac{V_{CC}-I_{Max}\times R_{Sense}}{I_{Max}}$
     $R_{LoadMax}=22.5\Omega =\frac{5V-200mA\times 2.5\Omega }{200mA}$
4. MOSFET selection:
   • Ensure that the MOSFET V_GS(th) can be driven by the op amp and that it can handle the power dissipation for the expected load resistance and maximum current:
     $P_{Q1}=V_{CC}\times I_{Max}-{I_{Max}}^2\times \left(R_{Load}+R_{Sense}\right)$
     $P_{Q1}=0.3W=5V\times 200mA-{\left(200mA\right)}^2\times \left(15\Omega +2.5\Omega \right)$
5. Current Sink Control Circuit
   
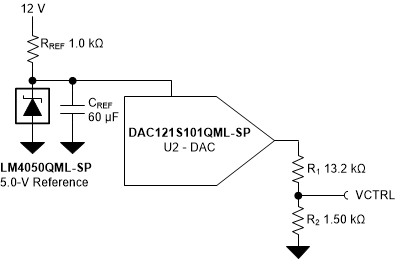
   • The DAC121S101QML-SP can provide a means of adjusting the voltage used to control the current sink.
   • The LM4050QML-SP provides a 5.0-V reference to the DAC. When C_REF = 60μF, the LM4050QML-SP is immune to SETs.
   • Since the DAC121S101QML-SP is a 12-bit DAC, it could have errors in the range of 10s of millivolts, which would dominate the system error. Therefore, the output voltage is scaled down by a factor of 5/49, given a maximum DAC operating voltage of 4.9V:
   $V_{DAC\left(max\right)}=4.9V\to V_{CTRL\left(max\right)}=500mV\to I_{LOAD\left(max\right)}=200mA$
   • Scaling down the voltage also means that any error introduced by the DAC121S101QML-SP or the LM4050QML-SP voltage reference are reduced by a factor of 5/49. Using a ratio of 5/49 also allows for the selection of standard 0.1% resistor values. The resistors introduce up to 0.179735% of error given the nominal resistor values and accounting for potential resistor value variation.
   • A key consideration for the system accuracy is the error introduced by the DAC and other devices. The error is often referred to as the Total Unadjusted Error (TUE) and is relative to the control voltage (V_CTRL) which is the dominant source of error for the circuit. In the circuit, the following error sources must be considered:
     • LM4050QML-SP 5.0-V Voltage Reference: Initial Accuracy, Drift over temperature (ΔVR/ΔT)
     • DAC121S101QML-SP DAC: Zero Code Error (ZEC), Gain Error (GE), ZEC Drift, and GE Drift
     • Resistor Divider (R1 and R2) Tolerance Error
     • LMP7704-SP: V_OS, I_OS, and I_BIAS
   • In this circuit, both Beginning of Life (BOL) and temperature tolerances are considered for calculating the V_CTRL TUE. Root Sum Square (RSS) is used to represent the added error of all sources. Error contributions from the voltage reference and the DAC are scaled by 5/49 in the TUE calculation.

   DAC	Data Sheet Specification	TUE T= 25°C	Data Sheet Specification	TUE ΔT = –55 to 125°C	TUE + Gain Calibration ΔT = –55 to 125°C
   INL (V)	2.75 LSB	3.357E-3	8.0 LSB	9.766E-3	9.766E-3
   DNL (V)	0.21 LSB	256.348E-6	1.0 LSB	1.221E-3	1.221E-3
   ZCE (V)	4 mV	4.000E-3	10 mV	10.000E-3	10.000E-3
   ZCE-Drift (V)			–20 µV/°C	–3.6E-3	–3.600E-3
   GE (V)	–0.11%	5.500E-3	1.00%	50.000E-3	1.221E-3
   GE-Drift (V)			–1 ppm/°C	–900.0E-6	–900.000E-6
   Volt. Ref.
   Initial Acc. (V)	0.23% at IR<1mA	11.500E-3	0.23% at IR<1mA	11.500E-3	9.000E-6
   ΔVR/ΔT (V)			34 ppm/°C	30.6E-3	30.600E-3
   Op Amp
   VOS (V)	±37 μV	37.000E-6	±500 μV	500.000E-6	500.000E-6
   IBIAS (A)	±200 fA	200.000E-12	±400 pA	400.000E-12	400.000E-12
   IBIAS × R2 (V)		300.000E-9		600.000E-9	600.000E-9
   VOSDrift (V)			±5 μV/°C	900.000E-6	900.000E-6
   Scaling Res.
   Resistor Div.		898.674E-6		898.674E-6	898.674E-6
   VCTRL RSS TUE (mV)		1.669E-3		6.420E-3	3.718E-3
   VCTRL RSS Error%		0.334%		1.284%	0.744%

   • The first TUE calculation does not include drift over temperature and achieves less than 1% accuracy. The next TUE calculation accounts for the variation in temperature for ΔT = 180°C (–55 to 125°C) as well as the extreme maximum and minimum values provided in each respective data sheet over temperature. Accounting for both extreme values as well as the effect of temperature drift on certain specifications, the second TUE calculation achieves less 2% TUE.
   • In the previous calculation the error is dominated by the Gain Error (GE) of the DAC, which over temperature and radiation can vary as much as 1.0%. The GE accounts for up to 50mV of error at the output of the DAC or 5.102mV when scaled by a factor of 5/49. Reduce this error, as well as the error introduced by the initial accuracy of the reference, by performing gain calibration. With gain calibration, the TUE is reduced to 3.718mV or 0.759% of V_CTRL. The calibration allows for the design to achieve 1.0% accuracy.
6. Compensation components selection:
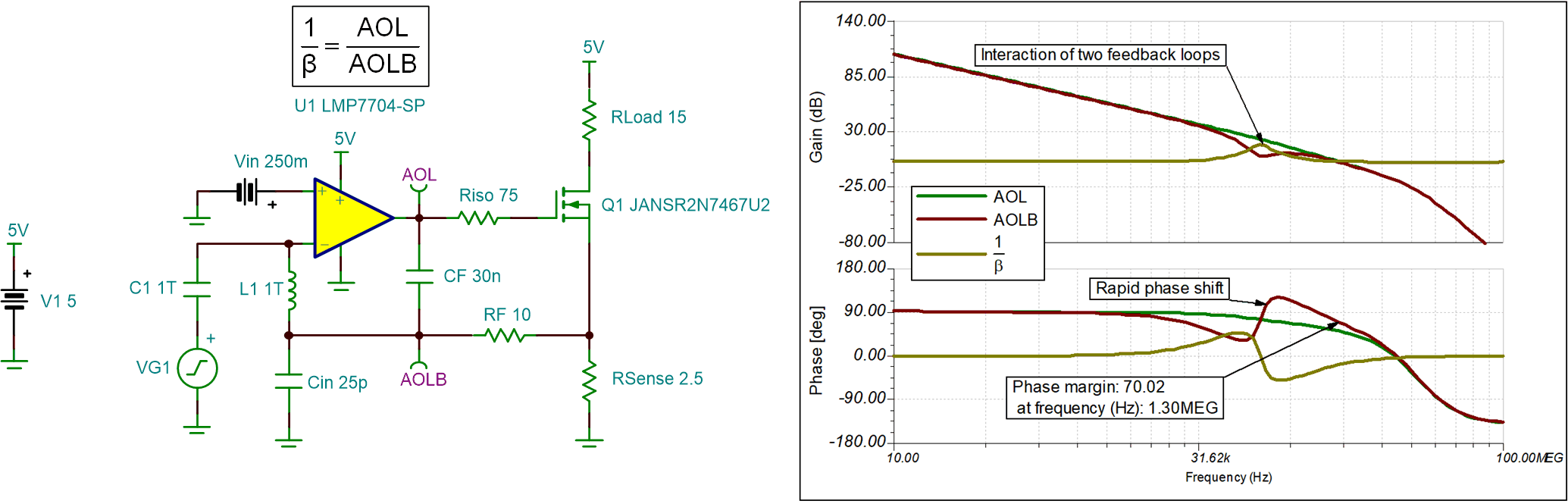
   • Stability analysis is done in the frequency domain and circuit stability is verified by the small signal transient step response. The criterion to ensure stability is a minimum phase margin of 45 degrees or a rate-of-closure (ROC) of 20dB/decade at fcl (loop gain, AOLB = 0dB) where the A_OL curve intersects 1/β.
   • The following open-loop AC simulation breaks the loop at the input and the following equations are used to plot the relevant curves:
   $A_{OL}=V_o\frac{1}{\beta }=\frac{V_o}{V_{FB}}{A}_{OL}\beta =V_{FB}$
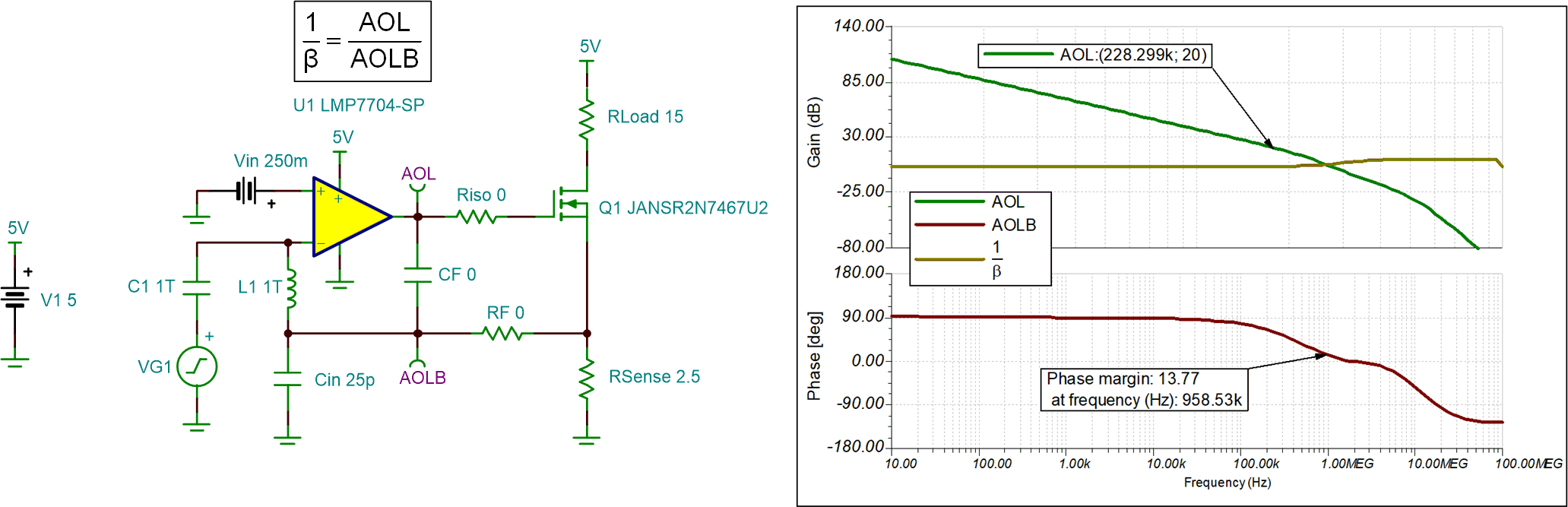
   • The following figure shows the open-loop AC response of the circuit if R_iso, RF, and CF are all zero (not in the circuit). The AOLB phase margin is 13.77° which indicates that the circuit is only marginally stable.
   • Cin is the equivalent input capacitance of the LMP7704-SP and is added due to the inductor L1 breaking the interaction of AOLB with the amplifier input capacitance.
     
     

     

     
     
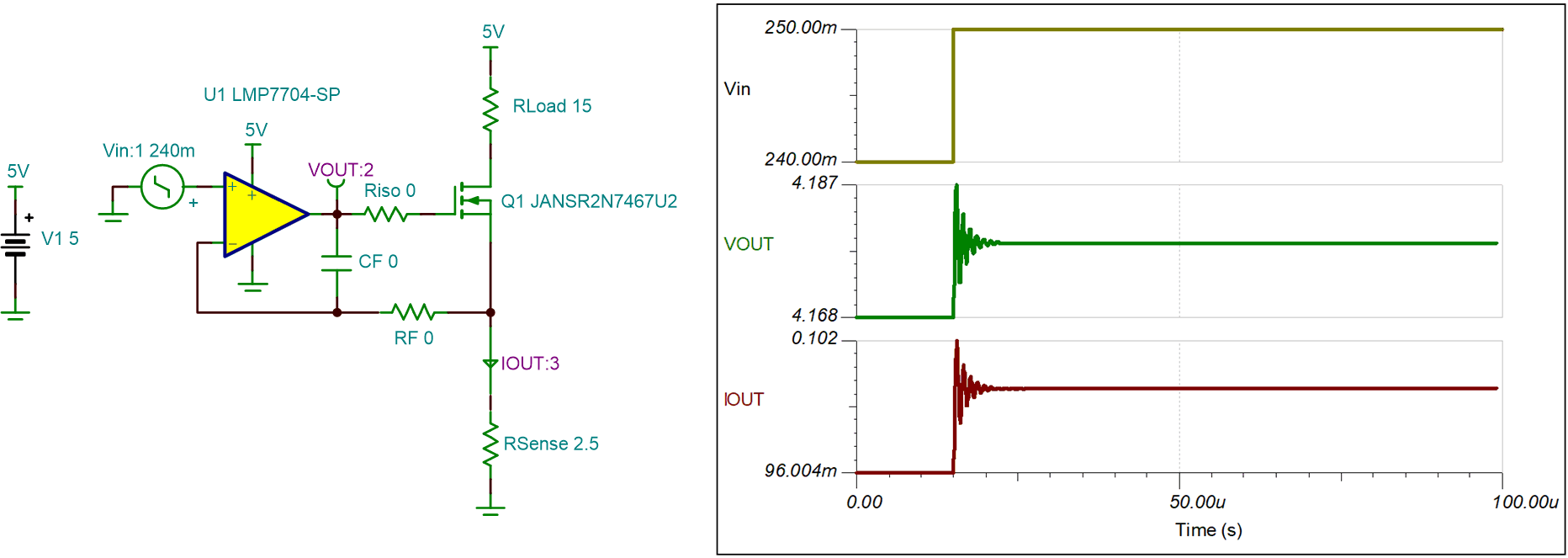
   • The AC simulation can be verified by the small signal step transient response. The small signal transient step response shows that the circuit has a long settling time with excessive ringing. Therefore, it is highly susceptible to oscillations.
     
     

     

     
     
   • The reason for the instability is: the op amp output impedance interacts with the MOSFET input capacitance and creates a pole in the AOL curve that causes a 40-dB/decade ROC. To compensate the circuit, start by finding the value for the isolation resistor R_iso, needed to mitigate the problem. Two things are needed to find R_iso, (1) the frequency where AOL is 20dB (f_20dBAOL), previously shown in the figure as 228.3kHz, (2) the input capacitance of the MOSFET which is found in the data sheet as 9.11nF. Then, use the following equation:
     $R_{iso}=\frac{1}{2\times \pi \times f_{20dBAOL}\times C_{load}}$
     $R_{iso}=75\Omega \approx \frac{1}{2\times \pi \times 228.3kHz\times 9.11nF}$
   • For more details on R_iso and driving capacitive loads, see TI Precision Labs - Op Amps: Stability - Capacitive loads.
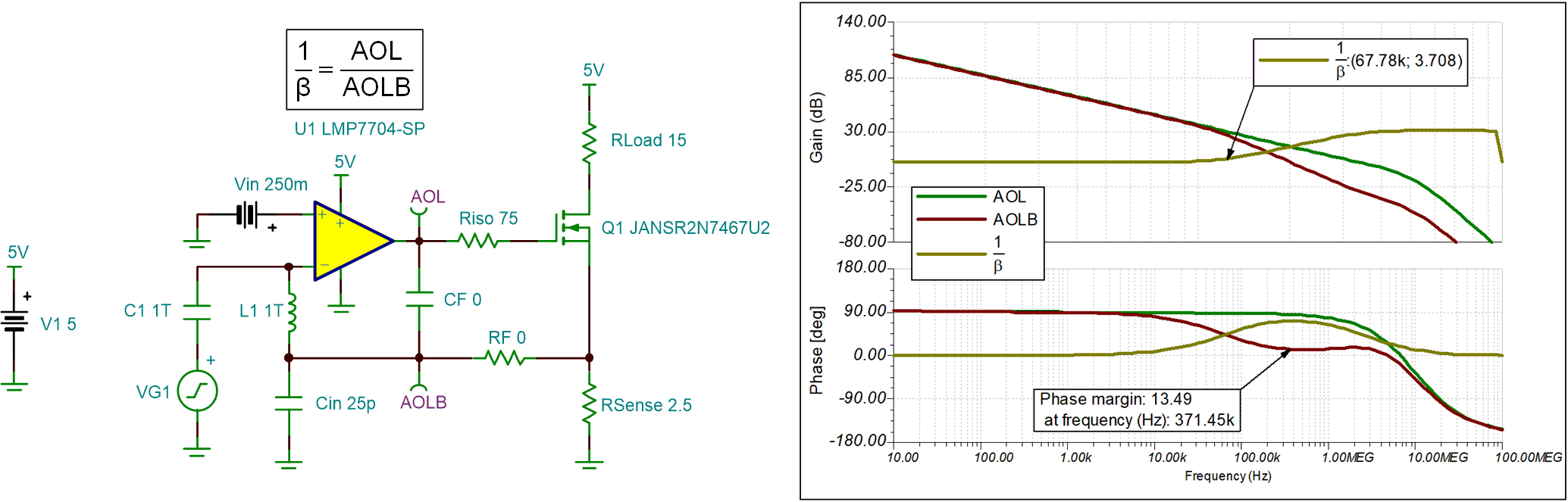
   • The new open loop AC response, after adding R_iso, is shown next. Even though the second pole in AOL was eliminated, the circuit remains only marginally stable due to a zero in 1/β caused by the delay from R_iso and the input capacitance of the MOSFET in the V-I loop.
     
     

     

     
     
   • The simple fix to this is to create a high frequency pole in 1/β and bypass the MOSFET at higher frequencies. By adding the capacitor CF, the amplifier returns to unity gain over the frequency range of interest. Calculate the value of CF by looking at the location of the 1/β zero (f_z1/β), shown in the previous figure as 67.78kHz. The value of CF is then calculated as:
     $CF=\frac{1}{2\times \pi \times R_{iso}\times \left(f_{z\frac{1}{\beta }}\right)}$
   • With CF added, the new open loop AC response looks like the following:
     
     

     

     
     
   • CF successfully formed the pole in 1/β; however, there is peaking in 1/β that causes instability. This occurs when CF interacts with the transconductance of the MOSFET. The effect of the interaction is two feedback loops to the amplifier. In this case, both feedback loops interact with each other around the resonant frequency. Adding a small value for RF (10Ω) can isolate the two feedback loops. With an RF of 10Ω, the circuit seems to have 70° of phase margin at fcl; however, in reality, it is still not stable. The next figure shows the instability through the rapid phase shifts in AOLB and the peaking in 1/β.
     
   • This may be confirmed by looking at the small signal transient step response which shows oscillation at the resonant frequency of about 170kHz for small values of RF.
     
     

     

     
     
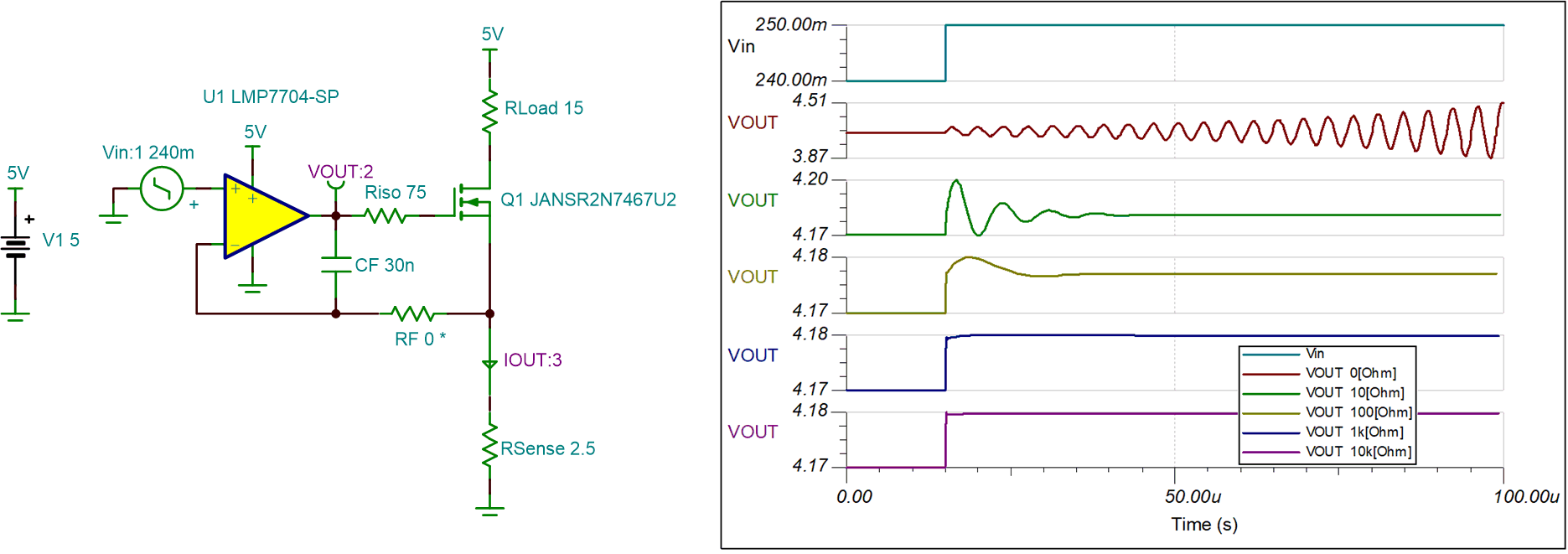
   • The final step to stabilizing the circuit is to add a sufficiently large resistor (RF) to flatten out 1/β and fully isolate CF from the MOSFET. Obtain the final value of RF through trial-and-error until the desired small signal step response is achieved. Typically, RF is in the range of 1kΩ to 10kΩ. The final open loop AC response is seen in the AC Simulation Results section. As seen from the previous simulation, different RF values yield different small signal step responses. With a zero or small RF value, oscillations and overshoot is observed. A value of 1kΩ for RF is sufficient to give the desired small signal transient response.