SNAA368 February 2023 HDC2010 , HDC2021 , HDC2022 , HDC2080 , HDC3020 , HDC3020-Q1 , HDC3021 , HDC3021-Q1 , HDC3022
1 Application Brief
Texas Instrument's digital temperature and relative humidity sensors measure the ambient environment which can be used for simple display or more importantly, assist in the command and control of environmental systems. In addition to providing these direct sensor measurements, there are several calculations which can be made (inside the system controller) from these sensor outputs which provide key results to maintain an environmental system and create the best operating and storage conditions for equipment. Calculations for dew point, absolute humidity, vapor saturation pressures of water, and enthalpy can be made from just ambient temperature and relative humidity measurements, as the purpose of this document is to support humidity applications for industrial and other relevant or related applications.
Vapor Pressure
There are two types of vapor pressure that are important to know: vapor pressure of water and the saturation vapor pressure. Vapor pressure of water is the pressure of water vapor in the air whereas the saturation vapor pressure is the pressure that water is in thermodynamic equilibrium with the condensed state. These values are important for the designer to know so that the environment can be gauged for how close the environment is to a condensing state. This measurement is an essential part of calculating the dew point. When the rate of evaporation is equal to the rate of condensation, the saturation vapor pressure can be measured. From this, it can be understood that saturation vapor pressure increases exponentially as the temperature increases.
#GUID-E01CC34B-3951-4658-882B-A73D1DED1CCD shows the calculation for saturation vapor pressure.
where
- T = temperature in °C
#GUID-168AAB8D-83AA-4C99-990F-8C40C8529EC9 shows the calculation for vapor pressure.
These values are used to calculate dew point.
Dew Point
The dew point is the temperature of the air that is cooled to reach a %RH of 100%. This means that the air cannot hold any more water and if the air was cooled down further, water vapor occurs in the form of condensation. Condensation is harmful to both the open cavity humidity sensor and the system the sensor is a part of, making it important to record the dew point to keep the sensor opening unblocked from condensation or water pooling on the top of the sensor. If the sensor is blocked and air cannot reach the sensor, inaccurate results can be reported, and if there is prolonged exposure outside the operating range of the relative humidity sensor, the device can lose precision. If the system is going to be in a condensing environment, the HDC3022 is a good choice due to the filter mounted on the top of the device, preventing any condensation from accumulating in the cavity. TI’s HDC2x and HDC3x devices include an alert feature that interrupts or wakes up the MCU that can be programmed to alert the user when nearing or passing the condensation point. This works to remove condensation by activating the on-chip heaters, bringing the %RH down to zero, or close to zero. However, to set this alert at an accurate %RH, the dew point must be calculated. See How TI Humidity Sensors Remove Device Condensation Using On-Chip Heaters.
Use #GUID-5F2F5B6C-BF91-47F8-B0BE-2DDA019F6A33 to calculate dew point.
where
- a = 17.625
- b = 243.04°C
In #GUID-5F2F5B6C-BF91-47F8-B0BE-2DDA019F6A33, a and b are known as Magnus coefficients.
#EQUATION-BLOCK_IQS_3P2_PVB is an alternative formula to find the vapor pressure of water using dew point:
Dew point can be used, for example, in aviation with regards to the automatic terminal information service (ATIS). ATIS is an automated service that reports the current aerodome information for aircraft that are both departing and arriving. Pilots use this service to learn about the current flying environment and dew point is one of the measures provided by ATIS. Pilots need the dew point because the humidity can affect their visibility; dew point that is close to the outside temperature means that there is high humidity, leading to potential fog. This serves as a warning to pilots who can prepare accordingly. Dew point is also used to determine the density altitude when combined with pressure and temperature. This measure indicates aircraft performance.
One important consideration is the dew point uncertainty when using a dew point mirror and the %RH measurement uncertainty. Using a constant value for dew point, the change in %RH uncertainty level is seen in #GUID-22483660-0001-4C1A-8351-5240311A95CF. In this particular example, the dew point mirror has a ±0.1°C uncertainty which leads to a ±0.6°C %RH uncertainty at higher %RH levels but lower uncertainty at lower %RH values. Additionally, the need for the two devices (device being tested and reference device) to be kept at the same temperature during testing is underscored by this graph, as otherwise there is an error in the %RH measurements being made.
Assuming the uncertainty of ±0.1°C of the dew point mirror, this graph shows that the %RH uncertainty increases at higher values.
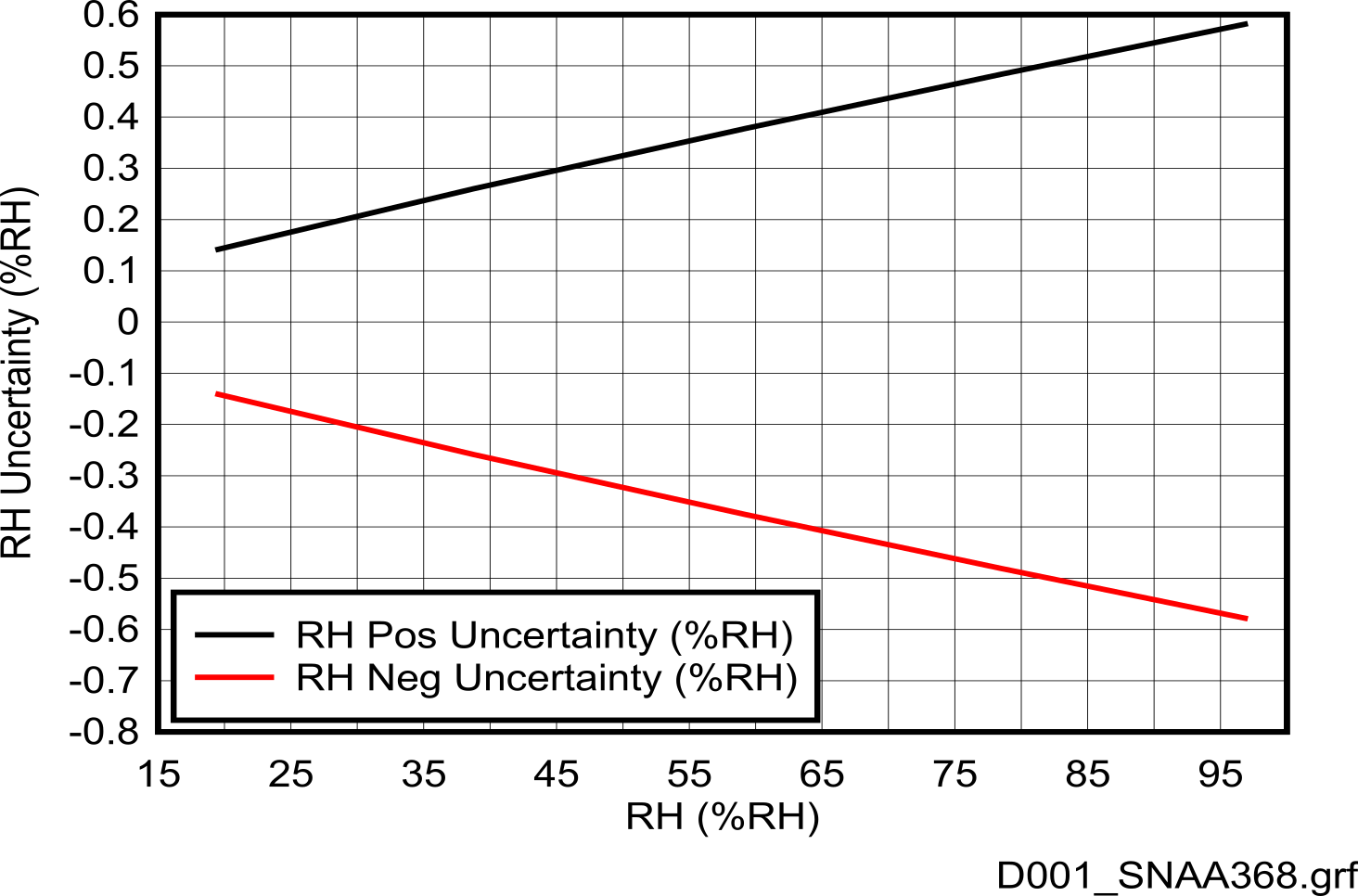 Figure 1-1 %RH Uncertainty vs %RH
Level
Figure 1-1 %RH Uncertainty vs %RH
LevelAbsolute Humidity
Absolute humidity is a simple calculation that tells the user the amount of water in the air, as opposed to relative humidity, the percentage of maximum water the air can hold. Depending on the use case for the system, knowing the absolute humidity can be used in reliability testing at higher temperatures. Absolute humidity is expressed in grams per cubic meter.
To calculate absolute humidity, the formula is:
For example, at an ambient temperature of 21°C and %RH of 50%, the absolute humidity is calculated to be approximately 9.155 g/m³.
Enthalpy
In humidity, enthalpy of the air includes the enthalpy of dry air and the enthalpy of the evaporated water in the air. Enthalpy is calculated when it is important to know the amount of heat that needs to be removed, a measure commonly seen in the HVAC industry. Enthalpy of the dry air is known as the sensible heat and enthalpy of the evaporated water is known as the latent heat and both make up the total enthalpy. To find the enthalpy, the mixing ratio must be calculated first. The mixing ratio is mass of water vapor over mass of dry gas. The ratio is calculated as follows:
Once the mixing ratio is calculated, enthalpy can be calculated from the mixing ratio using #EQUATION-BLOCK_DHP_ZQ2_PVB:
To convert to , do .
The importance of calculating enthalpy is seen in HVAC applications. Air conditioners absorb unwanted heat and release the heat outside to keep the inside of the building cool. The cooling is done in one of two ways: mechanical cooling which uses electricity to transfer the heat from the air stream to another medium or free cooling which uses outside conditions to bring heat to. Enthalpy comes into play when making the decision on which type of cooling to use since the outside air is a mix of dry air and water vapor. This means that the previously-described total enthalpy is used in calculations for the cooling process.
Conclusion
TI humidity sensors provide an accurate reading of relative humidity which can be extremely useful because additional information can be derived from this value. Using relative humidity, calculations of absolute humidity, dew point, vapor pressure, and enthalpy can be made to optimize the performance of the system. TI humidity sensors also come with the highest accuracy temperature sensor in the industry, which is not only the enabler to accurate relative humidity sensing, but also allows an accurate
temperature measurement that is crucial to the calculations shown in this application brief. References includes links to the Silicon User’s guide for both the HDC20XX and HDC30XX as well as a link to TI’s humidity sensing portfolio. Investigate these humidity sensors to determine the right device for your system.
References
- Texas Instruments, HDC20XX Silicon user's guide
- Texas Instruments, HDC30XX Silicon user's guide
- Texas Instruments, TI's Humidity Sensing Portfolio
- Texas Instruments, HDC302x 0.5%RH Digital Relative Humidity Sensor, 0.19%RH/yr Long Term Drift, 4s Response, Low-Power, Offset Error Correction, 0.1°C Temperature Sensor data sheet
- Texas Instruments, HDC3020EVM tool page
- Texas Instruments, How TI Humidity Sensors Remove Device Condensation Using On-Chip Heaters application brief