SBOA345 June 2021 ADC10D1000QML-SP , ADC12D1600QML-SP , ADC12D1620QML-SP , INA1620 , OPA132 , OPA134 , OPA1602 , OPA1604 , OPA1611 , OPA1612 , OPA1622 , OPA1632 , OPA1637 , OPA1641 , OPA1642 , OPA1644 , OPA1652 , OPA1654 , OPA1655 , OPA1656 , OPA1662 , OPA1664 , OPA1671 , OPA1677 , OPA1678 , OPA1679 , OPA1688 , OPA1692 , OPA2132 , OPA2134 , OPA4132 , OPA4134
3 Operational Amplifier Current Noise
As previously mentioned, amplifiers have a current noise contribution shown as IN in Figure 2-2. Current noise is represented as a noise source between the inverting and non-inverting inputs. Input current noise density (in) is most commonly shown in the amplifier data sheet in units of. For current noise calculations, it is often necessary to calculate Req, the equivalent resistance seen by the input, shown in Figure 3-1.
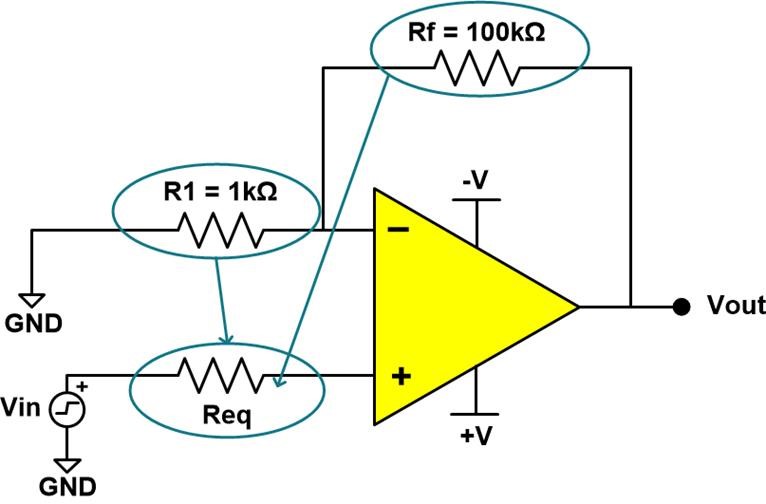Figure 3-1 Req Equivalent CircuitThe parallel combination of Rf and R1 act like a resistance on the amplifier’s non-inverting input, so Req in this example has a value of approximately 1kΩ.
This Req value can be multiplied by the input current noise density specification from the amplifier’s data sheet to yield the noise contribution due to current noise, in units of V/√Hz. This calculation is shown in Equation 3.
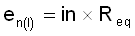
Multiplying the spectral density by the square root of the noise bandwidth gives RMS voltage noise. This is shown in Equation 4.
