SLOA011B January   2018  – July 2021 LF347 , LF353 , LM348 , MC1458 , TL022 , TL061 , TL062 , TL071 , TL072 , UA741

 

  1. 1Introduction
    1. 1.1 Amplifier Basics
    2. 1.2 Ideal Op Amp Model
  2. 2Non-Inverting Amplifier
    1. 2.1 Closed Loop Concepts and Simplifications
  3. 3Inverting Amplifier
    1. 3.1 Closed Loop Concepts and Simplifications
  4. 4Simplified Op Amp Circuit Diagram
    1. 4.1 Input Stage
    2. 4.2 Second Stage
    3. 4.3 Output Stage
  5. 5Op Amp Specifications
    1. 5.1  Absolute Maximum Ratings and Recommended Operating Condition
    2. 5.2  Input Offset Voltage
    3. 5.3  Input Current
    4. 5.4  Input Common Mode Voltage Range
    5. 5.5  Differential Input Voltage Range
    6. 5.6  Maximum Output Voltage Swing
    7. 5.7  Large Signal Differential Voltage Amplification
    8. 5.8  Input Parasitic Elements
      1. 5.8.1 Input Capacitance
      2. 5.8.2 Input Resistance
    9. 5.9  Output Impedance
    10. 5.10 Common-Mode Rejection Ratio
    11. 5.11 Supply Voltage Rejection Ratio
    12. 5.12 Supply Current
    13. 5.13 Slew Rate at Unity Gain
    14. 5.14 Equivalent Input Noise
    15. 5.15 Total Harmonic Distortion Plus Noise
    16. 5.16 Unity-Gain Bandwidth and Phase Margin
    17. 5.17 Settling Time
  6. 6References
  7. 7Glossary
  8. 8Revision History

1.1 Amplifier Basics

Before jumping into op amps, lets take a minute to review some amplifier fundamentals. An amplifier has an input port and an output port. In a linear amplifier, output signal = A × input signal, where A is the amplification factor or gain.

Depending on the nature of input and output signals, we can have four types of amplifier gain:

  • Voltage (voltage out/voltage in)
  • Current (current out/current in)
  • Transresistance (voltage out/current in)
  • Transconductance (current out/voltage in)

Since most op amps are voltage amplifiers, we will limit our discussion to voltage amplifiers.

Thevenin’s theorem can be used to derive a model of an amplifier, reducing it to the appropriate voltage sources and series resistances. The input port plays a passive role, producing no voltage of its own, and its Thevenin equivalent is a resistive element, Ri. The output port can be modeled by a dependent voltage source, AVi, with output resistance, Ro. To complete a simple amplifier circuit, we will include an input source and impedance, Vs and Rs, and output load, RL. Figure 1-1 shows the Thevenin equivalent of a simple amplifier circuit.

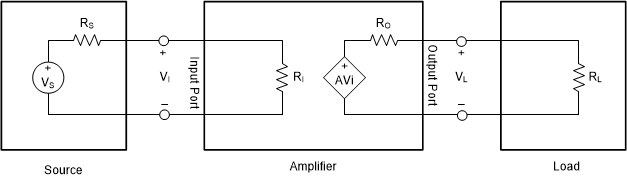GUID-9CEA5E6D-D0E5-44D9-A1B7-D15960686CE5-low.gifFigure 1-1 Thevenin Model of Amplifier with Source Load

It can be seen that we have voltage divider circuits at both the input port and the output port of the amplifier. This requires us to re-calculate whenever a different source and/or load is used and complicates circuit calculations.