SLVAE30E February   2021  – March 2021 TPS1H000-Q1 , TPS1H100-Q1 , TPS1H200A-Q1 , TPS1HA08-Q1 , TPS25200-Q1 , TPS27S100 , TPS2H000-Q1 , TPS2H160-Q1 , TPS2HB16-Q1 , TPS2HB35-Q1 , TPS2HB50-Q1 , TPS4H000-Q1 , TPS4H160-Q1

 

  1.   Trademarks
  2. 1Introduction
  3. 2Driving Resistive Loads
    1. 2.1 Background
    2. 2.2 Application Example
    3. 2.3 Why Use a Smart High Side Switch?
      1. 2.3.1 Accurate Current Sensing
      2. 2.3.2 Adjustable Current Limiting
    4. 2.4 Selecting the Right Smart High Side Switch
      1. 2.4.1 Power Dissipation Calculation
      2. 2.4.2 PWM and Switching Loss
  4. 3Driving Capacitive Loads
    1. 3.1 Background
    2. 3.2 Application Examples
    3. 3.3 Why Use a Smart High Side Switch?
      1. 3.3.1 Capacitive Load Charging
      2. 3.3.2 Inrush Current Mitigation
        1. 3.3.2.1 Capacitor Charging Time
      3. 3.3.3 Thermal Dissipation
      4. 3.3.4 Junction Temperature During Capacitive Inrush
      5. 3.3.5 Over Temperature Shutdown
      6. 3.3.6 Selecting the Correct Smart High Side Switch
  5. 4Driving Inductive Loads
    1. 4.1 Background
    2. 4.2 Application Examples
    3. 4.3 Why Use a Smart High Side Switch?
    4. 4.4 Turn-On Phase
    5. 4.5 Turn-Off Phase
      1. 4.5.1 Demagnetization Time
      2. 4.5.2 Instantaneous Power Losses During Demagnetization
      3. 4.5.3 Total Energy Dissipated During Demagnetization
      4. 4.5.4 Measurement Accuracy
      5. 4.5.5 Application Example
      6. 4.5.6 Calculations
      7. 4.5.7 Measurements
    6. 4.6 Selecting the Correct Smart High Side Switch
  6. 5Driving LED Loads
    1. 5.1 Background
    2. 5.2 Application Examples
    3. 5.3 LED Direct Drive
    4. 5.4 LED Modules
    5. 5.5 Why Use a Smart High Side Switch?
    6. 5.6 Open Load Detection
    7. 5.7 Load Current Sensing
    8. 5.8 Constant Current Source
      1. 5.8.1 Selecting the Correct Smart High Side Switch
  7. 6Appendix
    1. 6.1 Transient Thermal Impedance Data
    2. 6.2 Demagnitization Energy Capability Data
  8. 7References
  9. 8Revision History

4.5.4 Measurement Accuracy

Let’s compare Equation 54 to measured data to verify the calculations. In this example, a pure inductor mounted on an iron core was measured precisely and a single 24-V pulse was applied and then turned off. The inductive coil had a 200 mH inductance and a 5.6 Ω series resistance.

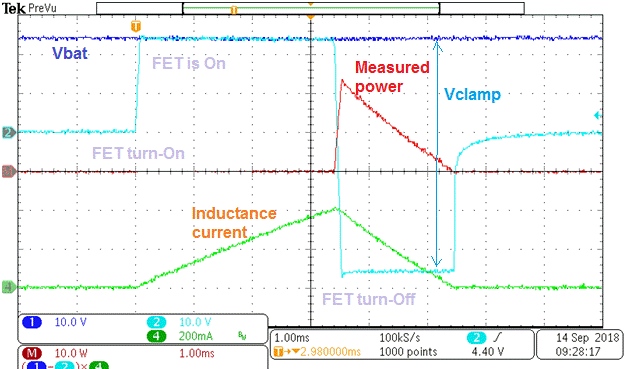GUID-0EDB3AC6-2CEC-44DF-A1E8-28510950B3CA-low.gifFigure 4-4 Demagnetization Energy During Inductive Turn-Off

Figure 4-4 shows both the turn-on and turn-off time. Looking at the turn-off time, we see that there is a TDEMAG of 3.3 ms and an I0 of 0.4 A. Table 4-1 compares these measured values to the values calculated from derived equations.

Table 4-1 Measured vs. Calculated Demagnetization Energy
InductancePeak CurrentVSUPPLYVCLAMPInductor EnergyDemagnetization EnergyDemagnetization Time
200 mH400 mA24 V60 V15.84Calculated26.4 mJ2.13 ms
Measured24 mJ2.05 ms

Table 4-1 shows the calculated demagnetization energy from Equation 54 is 26.4 mJ and the measured value is 24 mJ, less than 10% difference. This small difference is due to the approximations made during the derivation and measurement tolerances. The derived equations offer a good approximation of the inductive discharge energy.