SLVAE30E February   2021  – March 2021 TPS1H000-Q1 , TPS1H100-Q1 , TPS1H200A-Q1 , TPS1HA08-Q1 , TPS25200-Q1 , TPS27S100 , TPS2H000-Q1 , TPS2H160-Q1 , TPS2HB16-Q1 , TPS2HB35-Q1 , TPS2HB50-Q1 , TPS4H000-Q1 , TPS4H160-Q1

 

  1.   Trademarks
  2. 1Introduction
  3. 2Driving Resistive Loads
    1. 2.1 Background
    2. 2.2 Application Example
    3. 2.3 Why Use a Smart High Side Switch?
      1. 2.3.1 Accurate Current Sensing
      2. 2.3.2 Adjustable Current Limiting
    4. 2.4 Selecting the Right Smart High Side Switch
      1. 2.4.1 Power Dissipation Calculation
      2. 2.4.2 PWM and Switching Loss
  4. 3Driving Capacitive Loads
    1. 3.1 Background
    2. 3.2 Application Examples
    3. 3.3 Why Use a Smart High Side Switch?
      1. 3.3.1 Capacitive Load Charging
      2. 3.3.2 Inrush Current Mitigation
        1. 3.3.2.1 Capacitor Charging Time
      3. 3.3.3 Thermal Dissipation
      4. 3.3.4 Junction Temperature During Capacitive Inrush
      5. 3.3.5 Over Temperature Shutdown
      6. 3.3.6 Selecting the Correct Smart High Side Switch
  5. 4Driving Inductive Loads
    1. 4.1 Background
    2. 4.2 Application Examples
    3. 4.3 Why Use a Smart High Side Switch?
    4. 4.4 Turn-On Phase
    5. 4.5 Turn-Off Phase
      1. 4.5.1 Demagnetization Time
      2. 4.5.2 Instantaneous Power Losses During Demagnetization
      3. 4.5.3 Total Energy Dissipated During Demagnetization
      4. 4.5.4 Measurement Accuracy
      5. 4.5.5 Application Example
      6. 4.5.6 Calculations
      7. 4.5.7 Measurements
    6. 4.6 Selecting the Correct Smart High Side Switch
  6. 5Driving LED Loads
    1. 5.1 Background
    2. 5.2 Application Examples
    3. 5.3 LED Direct Drive
    4. 5.4 LED Modules
    5. 5.5 Why Use a Smart High Side Switch?
    6. 5.6 Open Load Detection
    7. 5.7 Load Current Sensing
    8. 5.8 Constant Current Source
      1. 5.8.1 Selecting the Correct Smart High Side Switch
  7. 6Appendix
    1. 6.1 Transient Thermal Impedance Data
    2. 6.2 Demagnitization Energy Capability Data
  8. 7References
  9. 8Revision History

4.5 Turn-Off Phase

Inductive loads seek to maintain continuous current flow in one direction. When an inductive load is turned off, the inductive load reverses the polarity of the applied voltage to prevent the immediate loss of current flow. That means if the voltage across the inductive load is positive during the on-phase, it will become negative when applied power is removed.

Immediately before the switch is opened, the load current I0 is equal to ILOAD,DC as calculated in Equation 31. Immediately after the switch opens the inductor current will begin decaying from I0 to zero as a continuous function. With a negative dI/dT and no applied VBAT, the voltage across the inductive load will invert and a negative voltage will appear on the high side switch output. This process is shown in Figure 4-3

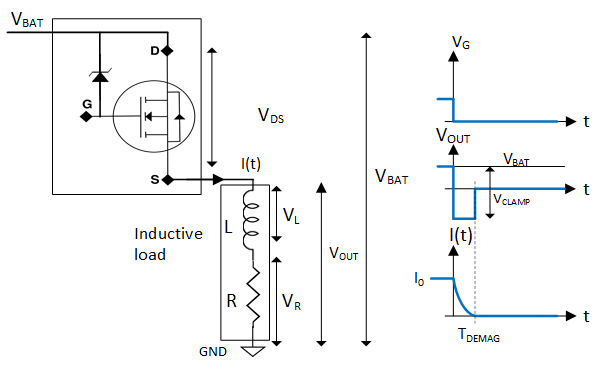GUID-664CCFFF-B533-4CF9-84F0-63E8D5A89BA6-low.gifFigure 4-3 Inductive Load Turn-Off Phase

Applying Kirchhoff’s voltage law gives Equation 33.

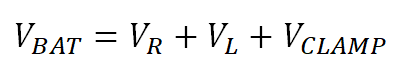
Equation 33. GUID-20200811-CA0I-TNX0-WMFK-4RS97P8BSFX6-low.png

Where VL is the voltage across the inductive element of the load, VR is the voltage across resistive element of the load, VCLAMP is the voltage across the switch FET VDS during a transient voltage spike, and VBAT is the supply voltage. Ohm’s law for resistors and inductors are seen in Equation 34 and Equation 35:

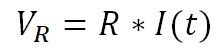
Equation 34. GUID-20200811-CA0I-Q2JK-R5MW-MGXPMWTZVKLF-low.png
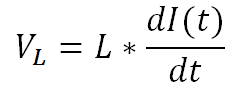
Equation 35. GUID-20200811-CA0I-LPSR-976Z-848DLMMZCXQX-low.png

Inserting those into Equation 33 gives Equation 36:

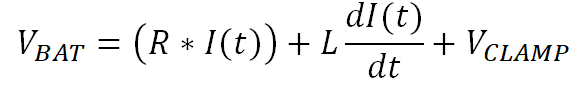
Equation 36. GUID-20200811-CA0I-T32M-SJZ6-PXKB9R4NCFBX-low.png

Rearranging Equation 36 gives Equation 37, which is a first order differential equation for the load current.

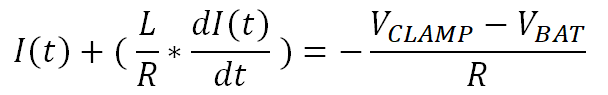
Equation 37. GUID-20200811-CA0I-VHPP-1XXD-VDMTTXNPGRMX-low.png

This is solved in Equation 38.

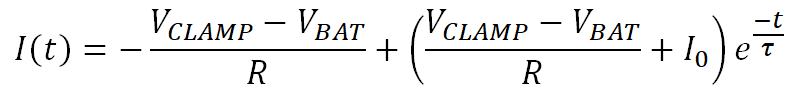
Equation 38. GUID-20200811-CA0I-XV06-JZSP-QBMWLP1XJPM7-low.png

Where I0 is the current when the switch is initially opened. Equation 38 shows that the current decays exponentially with negative slope and time constant τ = L/R. This equation serves as the basis for calculating the inductive load demagnetization energy. The current has two components: on the left side of the equation is the steady state current contribution and on the right is the transient current contribution that is modified by the exponential time factor. The load is demagnetized completely when the total current is zero and the two components are equal.

Note that Equation 38 is valid only from time t = 0 until the load is completely demagnetized. This demagnetization time is calculated in the next section.