SNVSAT9 June 2017 LM25145
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Description (continued)
- 6 Pin Configuration and Functions
- 7 Specifications
-
8 Detailed Description
- 8.1 Overview
- 8.2 Functional Block Diagram
- 8.3
Feature Description
- 8.3.1 Input Range (VIN)
- 8.3.2 Output Voltage Setpoint and Accuracy (FB)
- 8.3.3 High-Voltage Bias Supply Regulator (VCC)
- 8.3.4 Precision Enable (EN/UVLO)
- 8.3.5 Power Good Monitor (PGOOD)
- 8.3.6 Switching Frequency (RT, SYNCIN)
- 8.3.7 Configurable Soft-Start (SS/TRK)
- 8.3.8 Voltage-Mode Control (COMP)
- 8.3.9 Gate Drivers (LO, HO)
- 8.3.10 Current Sensing and Overcurrent Protection (ILIM)
- 8.3.11 OCP Duty Cycle Limiter
- 8.4 Device Functional Modes
-
9 Application and Implementation
- 9.1 Application Information
- 9.2 Typical Applications
- 10Power Supply Recommendations
- 11Layout
- 12Device and Documentation Support
- 13Mechanical, Packaging, and Orderable Information
Package Options
Refer to the PDF data sheet for device specific package drawings
Mechanical Data (Package|Pins)
- RGY|20
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9 Application and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
9.1 Application Information
9.1.1 Design and Implementation
To expedite the process of designing of a LM25145-based regulator for a given application, please use the LM25145 Quickstart Calculator available as a free download, as well as numerous LM25145 reference designs populated in TI Designs™ reference design library, or the designs provided in Typical Applications. The LM25145 is also WEBENCH® Designer enabled.
9.1.2 Power Train Components
Comprehensive knowledge and understanding of the power train components are key to successfully completing a synchronous buck regulator design.
9.1.2.1 Inductor
For most applications, choose an inductance such that the inductor ripple current, ΔIL, is between 30% and 40% of the maximum DC output current at nominal input voltage. Choose the inductance using Equation 7 based on a peak inductor current given by Equation 8.
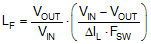
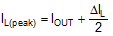
Check the inductor datasheet to ensure that the saturation current of the inductor is well above the peak inductor current of a particular design. Ferrite designs have very low core loss and are preferred at high switching frequencies, so design goals can then concentrate on copper loss and preventing saturation. Low inductor core loss is evidenced by reduced no-load input current and higher light-load efficiency. However, ferrite core materials exhibit a hard saturation characteristic and the inductance collapses abruptly when the saturation current is exceeded. This results in an abrupt increase in inductor ripple current, higher output voltage ripple, not to mention reduced efficiency and compromised reliability. Note that the saturation current of an inductor generally deceases as its core temperature increases. Of course, accurate overcurrent protection is key to avoiding inductor saturation.
9.1.2.2 Output Capacitors
Ordinarily, the output capacitor energy store of the regulator combined with the control loop response are prescribed to maintain the integrity of the output voltage within the dynamic (transient) tolerance specifications. The usual boundaries restricting the output capacitor in power management applications are driven by finite available PCB area, component footprint and profile, and cost. The capacitor parasitics—equivalent series resistance (ESR) and equivalent series inductance (ESL)—take greater precedence in shaping the load transient response of the regulator as the load step amplitude and slew rate increase.
The output capacitor, COUT, filters the inductor ripple current and provides a reservoir of charge for step-load transient events. Typically, ceramic capacitors provide extremely low ESR to reduce the output voltage ripple and noise spikes, while tantalum and electrolytic capacitors provide a large bulk capacitance in a relatively compact footprint for transient loading events.
Based on the static specification of peak-to-peak output voltage ripple denoted by ΔVOUT, choose an output capacitance that is larger than that given by Equation 9.
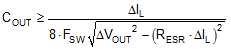
Figure 42 conceptually illustrates the relevant current waveforms during both load step-up and step-down transitions. As shown, the large-signal slew rate of the inductor current is limited as the inductor current ramps to match the new load-current level following a load transient. This slew-rate limiting exacerbates the deficit of charge in the output capacitor, which must be replenished as rapidly as possible during and after the load step-up transient. Similarly, during and after a load step-down transient, the slew rate limiting of the inductor current adds to the surplus of charge in the output capacitor that must be depleted as quickly as possible.
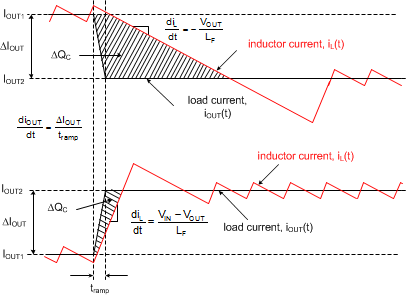 Figure 42. Load Transient Response Representation Showing COUT Charge Surplus or Deficit
Figure 42. Load Transient Response Representation Showing COUT Charge Surplus or Deficit
In a typical regulator application of 24-V input to low output voltage (for example, 5 V), it should be recognized that the load-off transient represents worst-case. In that case, the steady-state duty cycle is approximately 10% and the large-signal inductor current slew rate when the duty cycle collapses to zero is approximately –VOUT/L. Compared to a load-on transient, the inductor current takes much longer to transition to the required level. The surplus of charge in the output capacitor causes the output voltage to significantly overshoot. In fact, to deplete this excess charge from the output capacitor as quickly as possible, the inductor current must ramp below its nominal level following the load step. In this scenario, a large output capacitance can be advantageously employed to absorb the excess charge and limit the voltage overshoot.
To meet the dynamic specification of output voltage overshoot during such a load-off transient (denoted as ΔVOVERSHOOT with step reduction in output current given by ΔIOUT), the output capacitance should be larger than
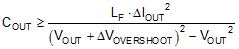
The ESR of a capacitor is provided in the manufacturer’s data sheet either explicitly as a specification or implicitly in the impedance vs. frequency curve. Depending on type, size and construction, electrolytic capacitors have significant ESR, 5 mΩ and above, and relatively large ESL, 5 nH to 20 nH. PCB traces contribute some parasitic resistance and inductance as well. Ceramic output capacitors, on the other hand, have low ESR and ESL contributions at the switching frequency, and the capacitive impedance component dominates. However, depending on package and voltage rating of the ceramic capacitor, the effective capacitance can drop quite significantly with applied DC voltage and operating temperature.
Ignoring the ESR term in Equation 9 gives a quick estimation of the minimum ceramic capacitance necessary to meet the output ripple specification. One to four 47-µF, 10-V, X7R capacitors in 1206 or 1210 footprint is a common choice. Use Equation 10 to determine if additional capacitance is necessary to meet the load-off transient overshoot specification.
A composite implementation of ceramic and electrolytic capacitors highlights the rationale for paralleling capacitors of dissimilar chemistries yet complementary performance. The frequency response of each capacitor is accretive in that each capacitor provides desirable performance over a certain portion of the frequency range. While the ceramic provides excellent mid- and high-frequency decoupling characteristics with its low ESR and ESL to minimize the switching frequency output ripple, the electrolytic device with its large bulk capacitance provides low-frequency energy storage to cope with load transient demands.
9.1.2.3 Input Capacitors
Input capacitors are necessary to limit the input ripple voltage to the buck power stage due to switching-frequency AC currents. TI recommends using X5R or X7R dielectric ceramic capacitors to provide low impedance and high RMS current rating over a wide temperature range. To minimize the parasitic inductance in the switching loop, position the input capacitors as close as possible to the drain of the high-side MOSFET and the source of the low-side MOSFET. The input capacitor RMS current is given by Equation 11.
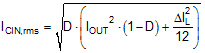
The highest input capacitor RMS current occurs at D = 0.5, at which point the RMS current rating of the capacitors should be greater than half the output current.
Ideally, the DC component of input current is provided by the input voltage source and the AC component by the input filter capacitors. Neglecting inductor ripple current, the input capacitors source current of amplitude (IOUT − IIN) during the D interval and sinks IIN during the 1−D interval. Thus, the input capacitors conduct a square-wave current of peak-to-peak amplitude equal to the output current. It follows that the resultant capacitive component of AC ripple voltage is a triangular waveform. Together with the ESR-related ripple component, the peak-to-peak ripple voltage amplitude is given by Equation 12.
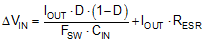
The input capacitance required for a particular load current, based on an input voltage ripple specification of ΔVIN, is given by Equation 13.
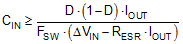
Low-ESR ceramic capacitors can be placed in parallel with higher valued bulk capacitance to provide optimized input filtering for the regulator and damping to mitigate the effects of input parasitic inductance resonating with high-Q ceramics. One bulk capacitor of sufficiently high current rating and two or three 2.2-μF 100-V X7R ceramic decoupling capacitors are usually sufficient. Select the input bulk capacitor based on its ripple current rating and operating temperature.
9.1.2.4 Power MOSFETs
The choice of power MOSFETs has significant impact on DC-DC regulator performance. A MOSFET with low on-state resistance, RDS(on), reduces conduction loss, whereas low parasitic capacitances enable faster transition times and reduced switching loss. Normally, the lower the RDS(on) of a MOSFET, the higher the gate charge and output charge (QG and QOSS respectively), and vice versa. As a result, the product RDS(on) × QG is commonly specified as a MOSFET figure-of-merit. Low thermal resistance ensures that the MOSFET power dissipation does not result in excessive MOSFET die temperature.
The main parameters affecting power MOSFET selection in an LM25145 application are as follows:
- RDS(on) at VGS = 7.5 V;
- Drain-source voltage rating, BVDSS, typically 30 V, 40 V or 60 V, depending on maximum input voltage;
- Gate charge parameters at VGS = 7.5 V;
- Output charge, QOSS, at the relevant input voltage;
- Body diode reverse recovery charge, QRR;
- Gate threshold voltage, VGS(th), derived from the plateau in the QG vs. VGS plot in the MOSFET data sheet. With a MOSFET Miller plateau voltage typically in the range of 3 V to 5 V, the 7.5-V gate drive amplitude of the LM25145 provides an adequately-enhanced MOSFET when on and a margin against Cdv/dt shoot-through when off.
The MOSFET-related power losses are summarized by the equations presented in Table 2, where suffixes 1 and 2 represent high-side and low-side MOSFET parameters, respectively. While the influence of inductor ripple current is considered, second-order loss modes, such as those related to parasitic inductances and SW node ringing, are not included. Consult the LM25145 Quickstart Calculator to assist with power loss calculations.
Table 2. Buck Regulator MOSFET Power Losses
| POWER LOSS MODE | HIGH-SIDE MOSFET | LOW-SIDE MOSFET |
|---|---|---|
| MOSFET Conduction(2)(3) | 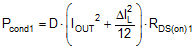 |
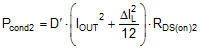 |
| MOSFET Switching | 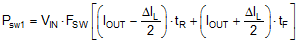 |
Negligible |
| MOSFET Gate Drive(1) | 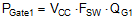 |
 |
| MOSFET Output Charge(4) | 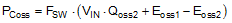 |
|
| Body Diode Conduction |
N/A | 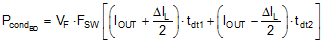 |
| Body Diode Reverse Recovery(5) |
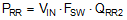 |
|
The high-side (control) MOSFET carries the inductor current during the PWM on-time (or D interval) and typically incurs most of the switching losses. It is therefore imperative to choose a high-side MOSFET that balances conduction and switching loss contributions. The total power dissipation in the high-side MOSFET is the sum of the losses due to conduction, switching (voltage-current overlap), output charge, and typically two-thirds of the net loss attributed to body diode reverse recovery.
The low-side (synchronous) MOSFET carries the inductor current when the high-side MOSFET is off (or 1–D interval). The low-side MOSFET switching loss is negligible as it is switched at zero voltage – current just commutates from the channel to the body diode or vice versa during the transition dead-times. The LM25145, with its adaptive gate drive timing, minimizes body diode conduction losses when both MOSFETs are off. Such losses scale directly with switching frequency.
In high step-down ratio applications, the low-side MOSFET carries the current for a large portion of the switching period. Therefore, to attain high efficiency, it is critical to optimize the low-side MOSFET for low RDS(on). In cases where the conduction loss is too high or the target RDS(on) is lower than available in a single MOSFET, connect two low-side MOSFETs in parallel. The total power dissipation of the low-side MOSFET is the sum of the losses due to channel conduction, body diode conduction, and typically one-third of the net loss attributed to body diode reverse recovery. The LM25145 is well suited to drive TI's comprehensive portfolio of NexFET™ power MOSFETs.
9.1.3 Control Loop Compensation
The poles and zeros inherent to the power stage and compensator are respectively illustrated by red and blue dashed rings in the schematic embedded in Table 3.
The compensation network typically employed with voltage-mode control is a Type-III circuit with three poles and two zeros. One compensator pole is located at the origin to realize high DC gain. The normal compensation strategy uses two compensator zeros to counteract the LC double pole, one compensator pole located to nullify the output capacitor ESR zero, with the remaining compensator pole located at one-half switching frequency to attenuate high frequency noise. The resistor divider network to FB determines the desired output voltage. Note that the lower feedback resistor, RFB2, has no impact on the control loop from an AC standpoint because the FB node is the input to an error amplifier and is effectively at AC ground. Hence, the control loop is designed irrespective of output voltage level. The proviso here is the necessary output capacitance derating with bias voltage and temperature.
Table 3. Buck Regulator Poles and Zeros(1)(2)
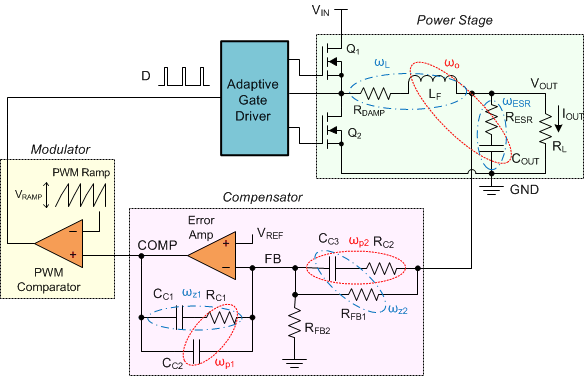
|
|||
|---|---|---|---|
| POWER STAGE POLES | POWER STAGE ZEROS | COMPENSATOR POLES | COMPENSATOR ZEROS |
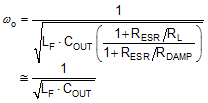 |
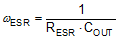 |
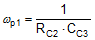 |
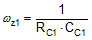 |
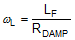 |
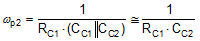 |
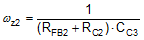 |
|
The small-signal open-loop response of a buck regulator is the product of modulator, power train and compensator transfer functions. The power stage transfer function can be represented as a complex pole pair associated with the output LC filter and a zero related to the ESR of the output capacitor. The DC (and low frequency) gain of the modulator and power stage is VIN/VRAMP. The gain from COMP to the average voltage at the input of the LC filter is held essentially constant by the PWM line feedforward feature of the LM25145 (15 V/V or 23.5 dB).
Complete expressions for small-signal frequency analysis are presented in Table 4. The transfer functions are denoted in normalized form. While the loop gain is of primary importance, a regulator is not specified directly by its loop gain but by its performance related characteristics, namely closed-loop output impedance and audio susceptibility.
Table 4. Buck Regulator Small-Signal Analysis
| TRANSFER FUNCTION | EXPRESSION |
|---|---|
| Open-loop transfer function | 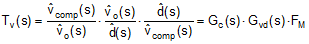 |
| Duty-cycle-to-output transfer function | 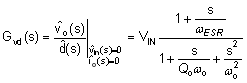 |
| Compensator transfer function(1) | 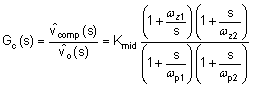 |
| Modulator transfer function | 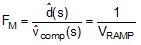 |
An illustration of the open-loop response gain and phase is given in Figure 43. The poles and zeros of the system are marked with x and o symbols, respectively, and a + symbol indicates the crossover frequency. When plotted on a log (dB) scale, the open-loop gain is effectively the sum of the individual gain components from the modulator, power stage, and compensator (see Figure 44). The open-loop response of the system is measured experimentally by breaking the loop, injecting a variable-frequency oscillator signal and recording the ensuing frequency response using a network analyzer setup.
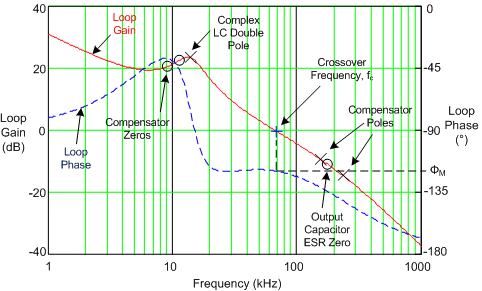 Figure 43. Typical Buck Regulator Loop Gain and Phase With Voltage-Mode Control
Figure 43. Typical Buck Regulator Loop Gain and Phase With Voltage-Mode Control
If the pole located at ωp1 cancels the zero located at ωESR and the pole at ωp2 is located well above crossover, the expression for the loop gain, Tv(s) in Table 4, can be manipulated to yield the simplified expression given in Equation 14.
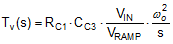
Essentially, a multi-order system is reduced to a single-order approximation by judicious choice of compensator components. A simple solution for the crossover frequency, denoted as fc in Figure 43, with Type-III voltage-mode compensation is derived as shown in Equation 15 and Equation 16.


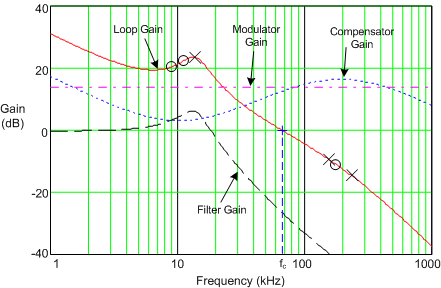 Figure 44. Buck Regulator Constituent Gain Components
Figure 44. Buck Regulator Constituent Gain Components
The loop crossover frequency is usually selected between one-tenth to one-fifth of switching frequency. Inserting an appropriate crossover frequency into Equation 15 gives a target for the mid-band gain of the compensator, Kmid. Given an initial value for RFB1, RFB2 is then selected based on the desired output voltage. Values for RC1, RC2, CC1, CC2 and CC3 are calculated from the design expressions listed in Table 5, with the premise that the compensator poles and zeros are set as follows: ωz1 = 0.5·ωo, ωz2 = ωo, ωp1 = ωESR, ωp2 = ωSW/2.
Table 5. Compensation Component Selection
| RESISTORS | CAPACITORS |
|---|---|
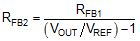 |
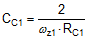 |
 |
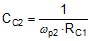 |
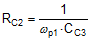 |
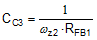 |
Referring to the bode plot in Figure 43, the phase margin, indicated as φM, is the difference between the loop phase and –180° at crossover. A target of 50° to 70° for this parameter is considered ideal. Additional phase boost is dialed in by locating the compensator zeros at a frequency lower than the LC double pole (hence why CC1 is scaled by a factor of 2 above). This helps mitigate the phase dip associated with the LC filter, particularly at light loads when the Q-factor is higher and the phase dip becomes especially prominent. The ramification of low phase in the frequency domain is an under-damped transient response in the time domain.
The power supply designer now has all the necessary expressions to optimally position the loop crossover frequency while maintaining adequate phase margin over the required line, load and temperature operating ranges. The LM25145 Quickstart Calculator is available to expedite these calculations and to adjust the bode plot as needed.
9.1.4 EMI Filter Design
Switching regulators exhibit negative input impedance, which is lowest at the minimum input voltage. An underdamped LC filter exhibits a high output impedance at the resonant frequency of the filter. For stability, the filter output impedance must be less than the absolute value of the converter input impedance.
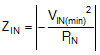
The EMI filter design steps are as follows:
- Calculate the required attenuation of the EMI filter at the switching frequency, where CIN represents the existing capacitance at the input of the switching converter;
- Input filter inductor LIN is usually selected between 1 μH and 10 μH, but it can be lower to reduce losses in a high current design;
- Calculate input filter capacitor CF.
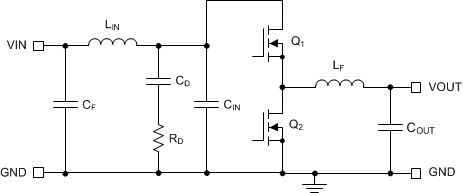 Figure 45. Buck Regulator With π-Stage EMI Filter
Figure 45. Buck Regulator With π-Stage EMI Filter
By calculating the first harmonic current from the Fourier series of the input current waveform and multiplying it by the input impedance (the impedance is defined by the existing input capacitor CIN), a formula is derived to obtain the required attenuation as shown by Equation 18.
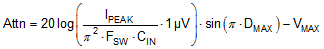
VMAX is the allowed dBμV noise level for the applicable EMI standard, for example EN55022 Class B. CIN is the existing input capacitance of the buck regulator, DMAX is the maximum duty cycle, and IPEAK is the peak inductor current. For filter design purposes, the current at the input can be modeled as a square-wave. Determine the EMI filter capacitance CF from Equation 19.
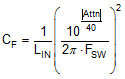
Adding an input filter to a switching regulator modifies the control-to-output transfer function. The output impedance of the filter must be sufficiently small such that the input filter does not significantly affect the loop gain of the buck converter. The impedance peaks at the filter resonant frequency. The resonant frequency of the filter is given by Equation 20.
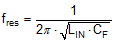
The purpose of RD is to reduce the peak output impedance of the filter at the resonant frequency. Capacitor CD blocks the DC component of the input voltage to avoid excessive power dissipation in RD. Capacitor CD should have lower impedance than RD at the resonant frequency with a capacitance value greater than that of the input capacitor CIN. This prevents CIN from interfering with the cutoff frequency of the main filter. Added damping is needed when the output impedance of the filter is high at the resonant frequency (Q of filter formed by LIN and CIN is too high). An electrolytic capacitor CD can be used for damping with a value given by Equation 21.
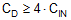
Select the damping resistor RD using Equation 22.
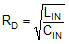
9.2 Typical Applications
 |
For step-by-step design procedure, circuit schematics, bill of materials, PCB files, simulation and test results of an LM25145-powered implementation, please refer to TI Designs reference design library. |
9.2.1 Design 1 – 20-A High-Efficiency Synchronous Buck Regulator for Telecom Power Applications
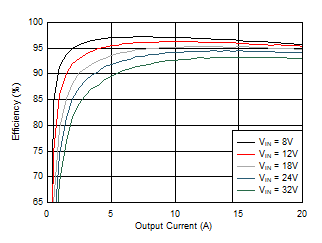
Figure 46 shows the schematic diagram of a 5-V, 20-A buck regulator with a switching frequency of 500 kHz. In this example, the target full-load efficiency is 94% at a nominal input voltage of 24 V that ranges from 6.5 V to as high as 32 V. The switching frequency is set by means of a synchronization input signal at 500 kHz, and the free-running switching frequency (in the event that the synchronization signal is removed) is set at 450 kHz by resistor RRT. In terms of control loop performance, the target loop crossover frequency is 70 kHz with a phase margin greater than 50°. The output voltage soft-start time is 4 ms.
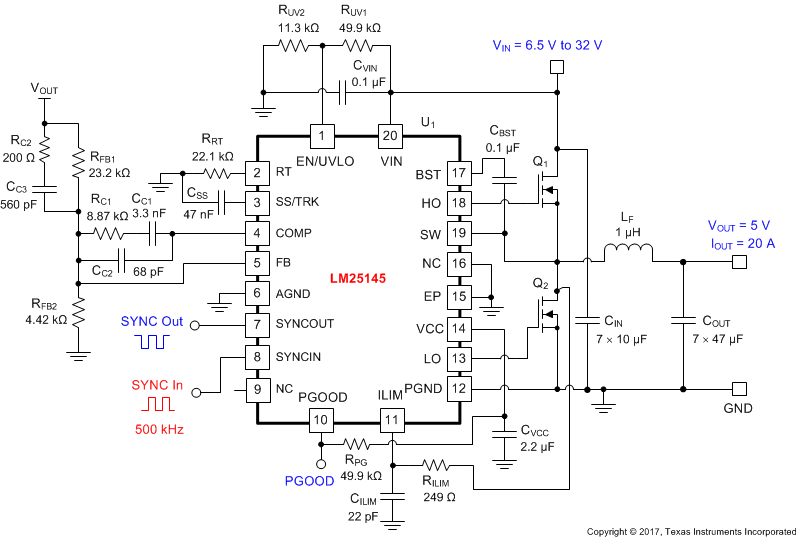 Figure 46. Application Circuit #1 With LM25145 24-V to 5-V, 20-A Buck Regulator at 500 kHz
Figure 46. Application Circuit #1 With LM25145 24-V to 5-V, 20-A Buck Regulator at 500 kHz
NOTE
This and subsequent design examples are provided herein to showcase the LM25145 controller in several different applications. Depending on the source impedance of the input supply bus, an electrolytic capacitor may be required at the input to ensure stability, particularly at low input voltage and high output current operating conditions. See Power Supply Recommendations for more detail.
9.2.1.1 Design Requirements
The intended input, output, and performance-related parameters pertinent to this design example are shown in Table 6.
Table 6. Design Parameters
| DESIGN PARAMETER | VALUE |
|---|---|
| Input voltage range (steady-state) | 6.5 V to 32 V |
| Input transient voltage (peak) | 42 V |
| Output voltage and current | 5 V, 20 A |
| Input voltage UVLO thresholds | 6.5 V on, 6 V off |
| Switching frequency (SYNC in) | 500 kHz |
| Output voltage regulation | ±1% |
| Load transient peak voltage deviation | < 100 mV |
9.2.1.2 Detailed Design Procedure
The design procedure for an LM25145-based regulator for a given application is streamlined by using the LM25145 Quickstart Calculator available as a free download, or by availing of TI's WEBENCH® Power Designer.
The selected buck converter powertrain components are cited in Table 7, and many of the components are available from multiple vendors. The MOSFETs in particular are chosen for both lowest conduction and switching power loss, as discussed in detail in Power MOSFETs.
The current limit setpoint in this design is set at 26 A based on the resistor RILIM and the 2-mΩ RDS(on) of the low-side MOSFET (typical at TJ = 25°C and VGS = 7.5 V). This design uses a low-DCR, metal-powder inductor and an all-ceramic output capacitor implementation.
Table 7. List of Materials for Design 1
| REFERENCE DESIGNATOR | QTY | SPECIFICATION | MANUFACTURER | PART NUMBER |
|---|---|---|---|---|
| CIN | 7 | 10 µF, 50 V, X7R, 1210, ceramic | TDK | C3225X7R1H106M |
| Murata | GRM32ER71H106KA12L | |||
| AVX | 12105C106KAT2A | |||
| Kemet | C1210C106K5RACTU | |||
| Taiyo Yuden | UMK325AB7106MM-T | |||
| COUT | 7 | 47 µF, 10 V, X7R, 1210, ceramic | Murata | GRM32ER71A476KE15L |
| Taiyo Yuden | LMK325B7476MM-TR | |||
| AVX | 1210ZC476KAT2A | |||
| Kemet | C1210C476M8RAC7800 | |||
| LF | 1 | 1 µH, 2.3 mΩ, 40 A, 11.15 × 10 × 3.8 mm | Cyntec | CMLE104T-1R0MS2R307 |
| 1.2 µH, 1.8 mΩ, 25 A, 10.2 × 10.2 × 4.7 mm | Würth Electronik | WE HCI 744325120 | ||
| 1 µH, 2.3 mΩ, 38 A, 10.9 × 10 × 5.0 mm | Panasonic | ETQP5M1R0YLC | ||
| 1 µH, 2.2 mΩ, 36 A, 10.5 × 10 × 6.5 mm | TDK | SPM10065VT-D | ||
| Q1 | 1 | 40 V, 3.7 mΩ, high-side MOSFET, SON 5 × 6 | Texas Instruments | CSD18503Q5A |
| Q2 | 1 | 40 V, 2 mΩ, low-side MOSFET, SON 5 × 6 | Texas Instruments | CSD18511Q5A |
| U1 | 1 | Wide VIN synchronous buck controller | Texas Instruments | LM25145RGYR |
9.2.1.3 Custom Design With WEBENCH® Tools
Click here to create a custom design using the LM25145 device with the WEBENCH® Power Designer.
- Start by entering the input voltage (VIN), output voltage (VOUT), and output current (IOUT) requirements.
- Optimize the design for key parameters such as efficiency, footprint, and cost using the optimizer dial.
- Compare the generated design with other possible solutions from Texas Instruments.
The WEBENCH Power Designer provides a customized schematic along with a list of materials with real-time pricing and component availability.
In most cases, these actions are available:
- Run electrical simulations to see important waveforms and circuit performance
- Run thermal simulations to understand board thermal performance
- Export customized schematic and layout into popular CAD formats
- Print PDF reports for the design, and share the design with colleagues
Get more information about WEBENCH tools at www.ti.com/WEBENCH.
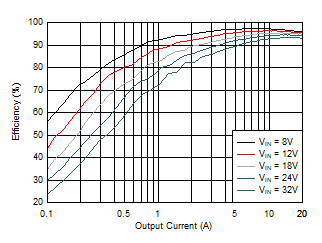
9.2.1.4 Application Curves
| SYNCIN tied to VCC | ||
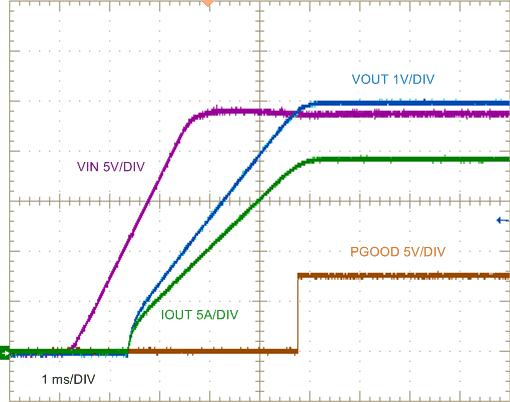
| VIN step to 24 V | 0.25-Ω Load |
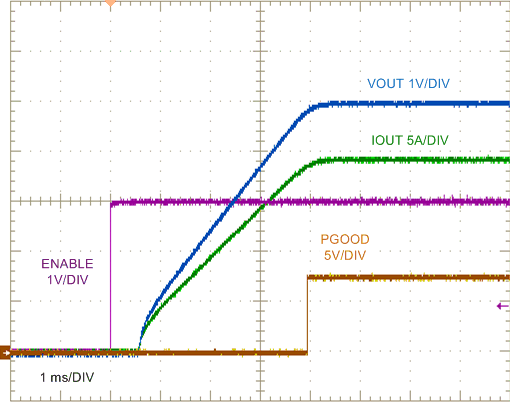
| VIN = 24 V | 0.25-Ω Load |
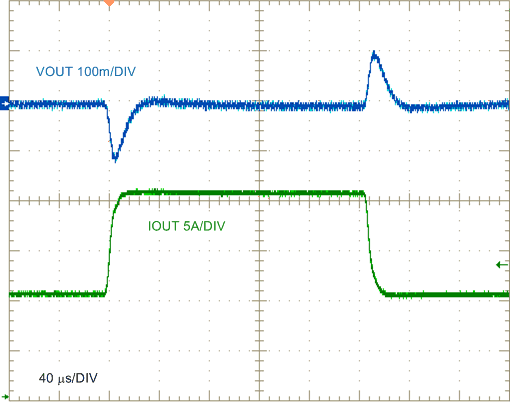
| VIN = 24 V |
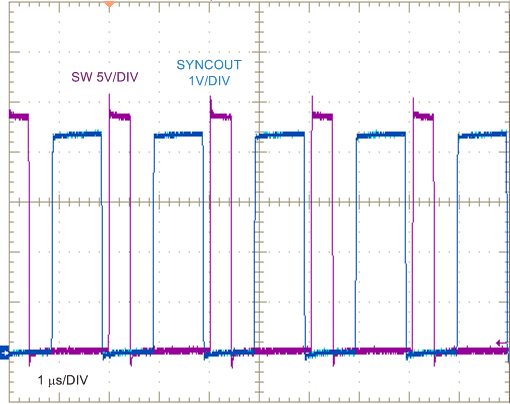
| VIN = 24 V | IOUT = 0 A |
| SYNCIN tied to GND | ||
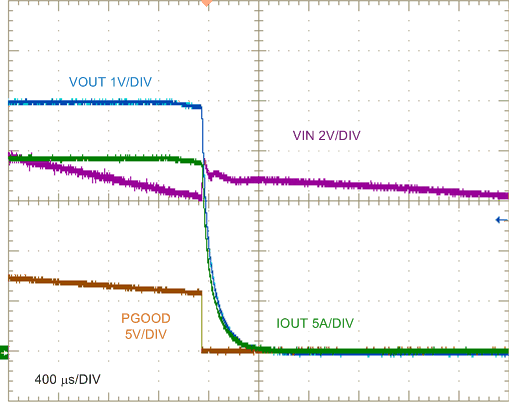
| VIN 24 V to 6 V | 0.25-Ω Load |

| VIN = 24 V | 0.25-Ω Load |
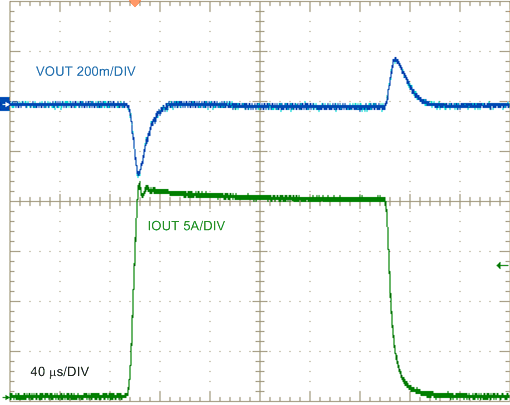
| VIN = 24 V |
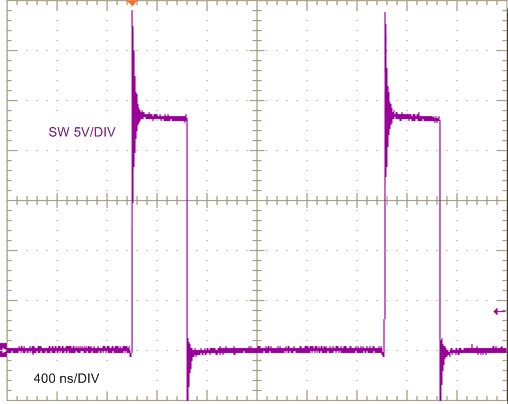
| VIN = 24 V | IOUT = 20 A |
9.2.2 Design 2 – High Density, 12-V, 8-A Rail With LDO Low-Noise Auxiliary Output for Industrial Applications
Figure 57 shows the schematic diagram of a 425-kHz, 12-V output, 8-A synchronous buck regulator intended for RF power applications.
An auxiliary 10-V, 800-mA rail to power noise-sensitive circuits is available using the LP38798 ultra-low noise LDO as a post-regulator. The internal pullup of the EN pin of the LP38798 facilitates direct connection to the PGOOD of the LM25145 for sequential start-up control.
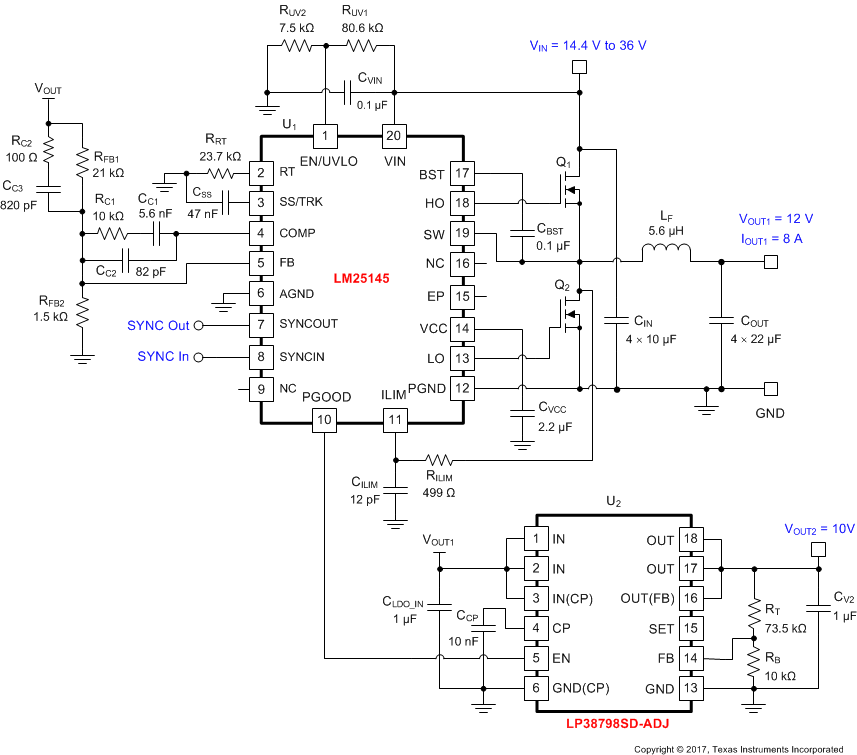 Figure 57. Application Circuit #2 With LM25145 24-V to 12-V Synchronous Buck Regulator at 425 kHz
Figure 57. Application Circuit #2 With LM25145 24-V to 12-V Synchronous Buck Regulator at 425 kHz
9.2.2.1 Design Requirements
The required input, output, and performance parameters for this application example are shown in Table 8.
Table 8. Design Parameters
| DESIGN PARAMETER | VALUE |
|---|---|
| Input voltage range (steady-state) | 14.4 V to 36 V |
| Input transient voltage (peak) | 42 V |
| Output voltage and current | 12 V, 8 A |
| Input UVLO thresholds | 14 V on, 13.2 V off |
| Switching frequency | 425 kHz |
| Output voltage regulation | ±1% |
| Load transient peak voltage deviation, 4-A load step, 1 A/µs | < 150 mV |
9.2.2.2 Detailed Design Procedure
A high power density, high-efficiency regulator solution is realized by using TI NexFET™ Power MOSFETs, such as CSD18543Q3A (60-V, 8.5-mΩ MOSFET in a SON 3.3-mm × 3.3-mm package), together with a low-DCR inductor and all-ceramic capacitor design. The design occupies 15 mm × 15 mm on a single-sided PCB. The overcurrent (OC) setpoint in this design is set at 11 A based on the resistor RILIM and the 8.5-mΩ RDS(on) of the low-side MOSFET (typical at TJ = 25°C and VGS = 7.5 V). Connecting VCC to either VOUT1 or VOUT2 using a series diode reduces bias power dissipation and improves efficiency, especially at light loads.
The selected buck converter powertrain components are cited in Table 9, including power MOSFETs, buck inductor, input and output capacitors, and ICs. Using the LM25145 Quickstart Calculator, compensation components are selected based on a target loop crossover frequency of 70 kHz and phase margin greater than 55°. The output voltage soft-start time is 4 ms based on the selected soft-start capacitance, CSS, of 47 nF.
Table 9. List of Materials for Design 2
| REFERENCE DESIGNATOR | QTY | SPECIFICATION | MANUFACTURER | PART NUMBER |
|---|---|---|---|---|
| CIN | 4 | 10 µF, 50 V, X7R, 1210, ceramic | TDK | C3225X7R1H106M |
| Murata | GRM32ER71H106KA12L | |||
| AVX | 12105C106KAT2A | |||
| COUT | 4 | 22 µF, 25 V, X7R, 1210, ceramic | Murata | GRM32ER71E226KE15L |
| Taiyo Yuden | TMK325B7226MM-TR | |||
| TDK | C3225X7R1E226M | |||
| LF | 1 | 5.6 µH, 17 mΩ, 18 A, 10.85 × 10 × 3.8 mm | Cyntec | CMLS104T-5R6MS |
| 5.6 µH, 20 mΩ, 14 A, 10.85 × 10 × 3.8 mm | Delta | MPT1040-5R6H1 | ||
| 5.6 µH, 16 mΩ, 12 A, 10.7 × 10 × 4 mm | Bourns | SRP1040-5R6M | ||
| 5.6 µH, 19.3 mΩ, 16 A, 11 × 10 × 4 mm | Laird | MGV10045R6M-10 | ||
| 6.8 µH, 17.5 mΩ, 14 A, 11 × 10 × 3.8 mm | Würth Electronik | WE-LHMI 74437368068 | ||
| 6.8 µH, 17.9 mΩ, 25 A, 10.5 × 10 × 4 mm | TDK | SPM10040VT-6R8M-D | ||
| 6.8 µH, 18.3 mΩ, 12.1 A, 10.7 × 10 × 4 mm | Panasonic | ETQP4M6R8KVC | ||
| Q1, Q2 | 2 | 60 V, 8 mΩ, MOSFET, SON 3 × 3 | Texas Instruments | CSD18543Q3A |
| U1 | 1 | Wide VIN synchronous buck controller | Texas Instruments | LM25145RGYR |
| U2 | 1 | Ultra-low noise and high-PSRR LDO for RF and analog circuits, 4-mm × 4-mm 12-pin WSON | Texas Instruments | LP38798SD-ADJ |
If needed, a 2.2-Ω resistor can be added in series with CBST is used to slow the turn-on transition of the high-side MOSFET, reducing the spike amplitude and ringing of the SW node voltage and minimizing the possibility of Cdv/dt-induced shoot-through of the low-side MOSFET. If needed, place an RC snubber (for example, 2.2 Ω and 100 pF) close to the drain (SW node) and source (PGND) terminals of the low-side MOSFET to further attenuate any SW node voltage overshoot and/or ringing. Please refer to the application note Reduce Buck Converter EMI and Voltage Stress by Minimizing Inductive Parasitics for more detail.
9.2.2.2.1 Application Curves
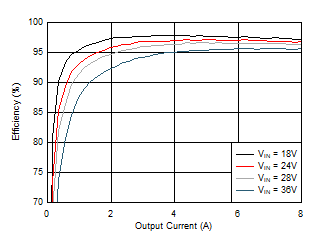
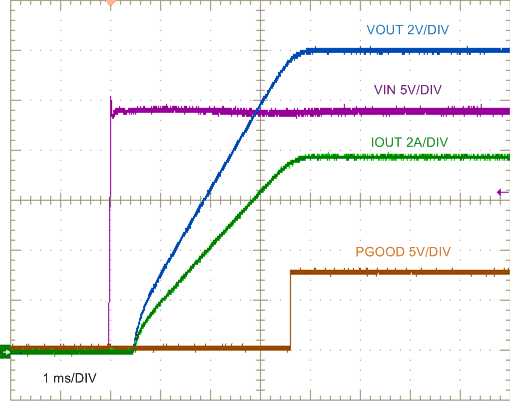
| VIN step to 24 V | 1.5-Ω Load |
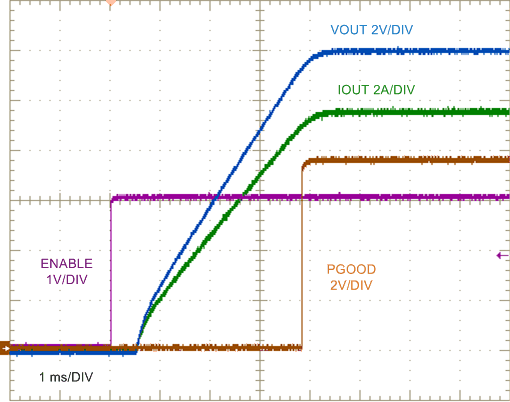
| VIN = 24 V | 1.5-Ω Load |
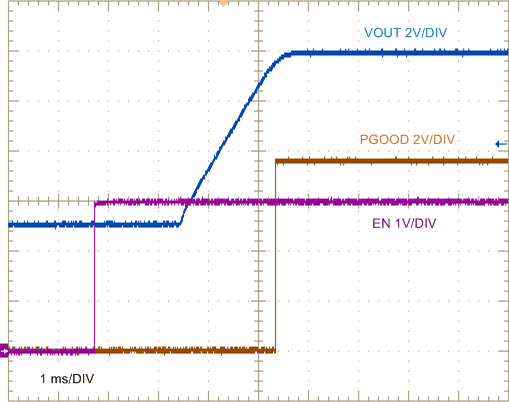
| VIN = 24 V | IOUT = 0 A |

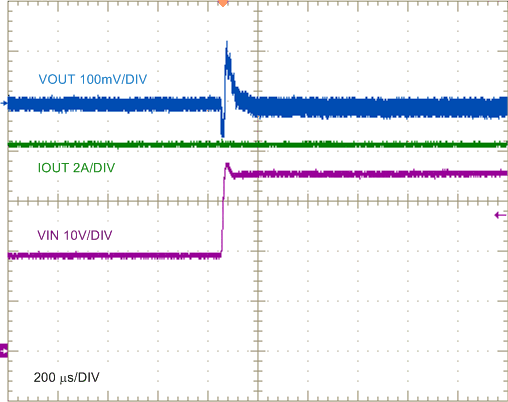
| VIN = 24 V |
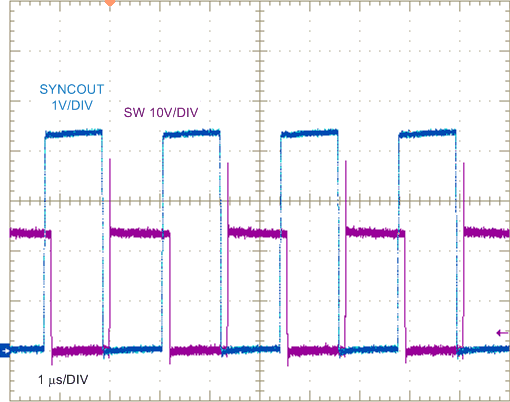
| IOUT = 8 A |
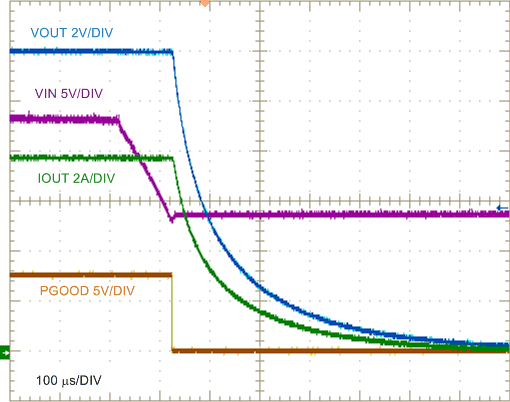
| VIN = 24 V | IOUT = 4 A |
| 1.5-Ω Load |
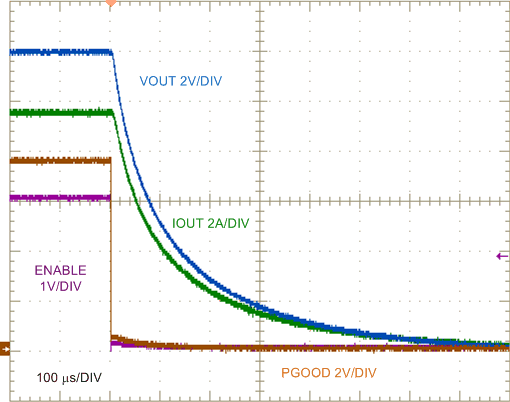
| VIN = 24 V | 1.5-Ω Load |
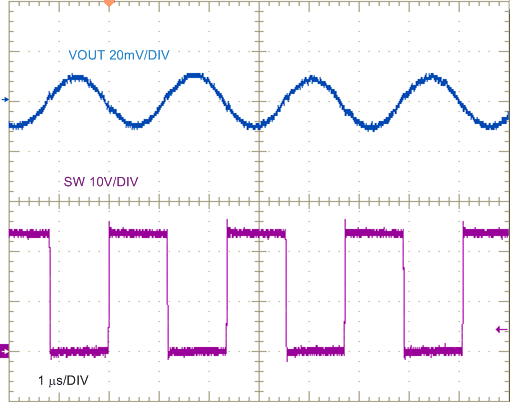
| VIN = 24 V | IOUT = 0 A |
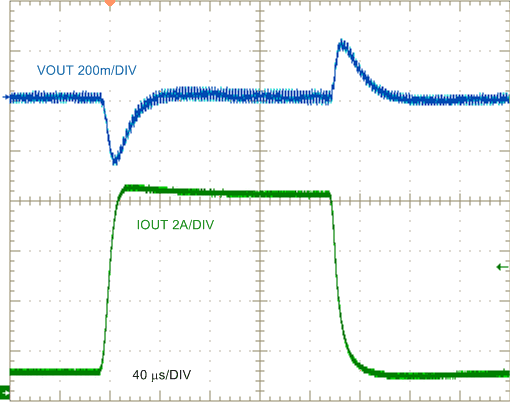
| VIN = 24 V |
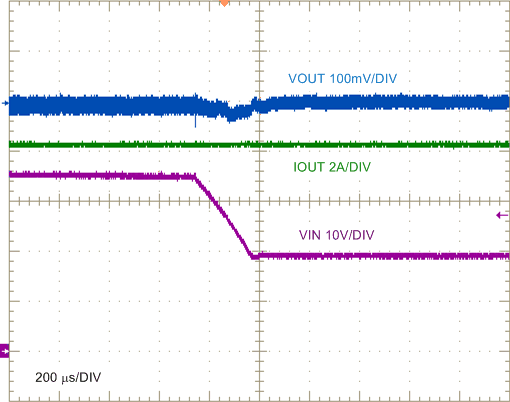
| IOUT = 8 A |
9.2.3 Design 3 – Powering a Multicore DSP From a 24-V Rail
 |
For technical solutions, industry trends, and insights for designing and managing power supplies, please refer to TI's Power House blog series. |
Figure 70 shows the schematic diagram of a 10-A synchronous buck regulator for a DSP core voltage supply.
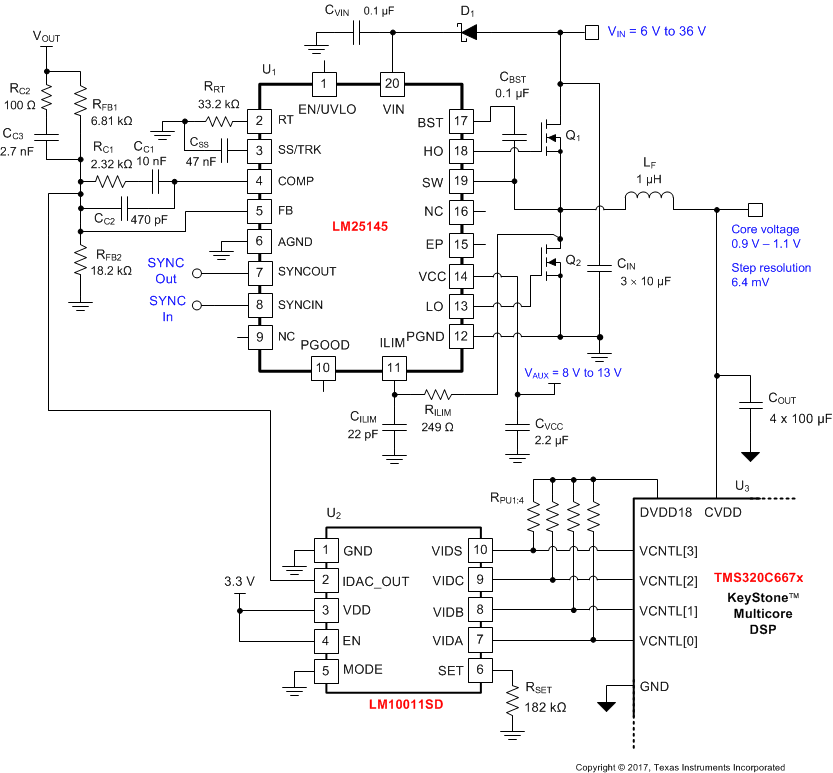 Figure 70. Application Circuit #3 With LM25145 DSP Core Voltage Supply
Figure 70. Application Circuit #3 With LM25145 DSP Core Voltage Supply
9.2.3.1 Design Requirements
For this application example, the intended input, output, and performance parameters are listed in Table 10.
Table 10. Design Parameters
| DESIGN PARAMETER | VALUE |
|---|---|
| Input voltage range (steady-state) | 6 V to 36 V |
| Input transient voltage (peak) | 42 V |
| Output voltage and current | 0.9 V to 1.1 V, 10 A |
| Output voltage regulation | ±1% |
| Load transient peak voltage deviation, 10-A step | < 120 mV |
| Switching frequency | 300 kHz |
9.2.3.2 Detailed Design Procedure
The schematic diagram of a 300-kHz, 24-V nominal input, 10-A regulator powering a KeyStone™ DSP is given in Figure 70. This high step-down ratio design leverages the low 40-ns minimum controllable on-time of the LM25145 controller to achieve stable, efficient operation at very low duty cycles. 60-V power MOSFETs, such as TI's CSD18543Q3A and CSD18531Q5A NexFET devices, are used together with a low-DCR, metal-powder inductor, and ceramic output capacitor implementation. An external rail between 8 V and 13 V powers VCC to minimize bias power dissipation, and a blocking diode connected to the VIN pin is used as recommended in Figure 32.
The important components for this design are listed in Table 11.
Table 11. List of Materials for Design 3
| REFERENCE DESIGNATOR | QTY | SPECIFICATION | MANUFACTURER | PART NUMBER |
|---|---|---|---|---|
| CIN | 3 | 10 µF, 50 V, X7R, 1210, ceramic | TDK | C3225X7R1H106M |
| Murata | GRM32ER71H106KA12L | |||
| AVX | 12105C106KAT2A | |||
| COUT | 4 | 100 µF, 6.3V, X7S, 1210, ceramic | Murata | GRM32EC70J107ME15L |
| Taiyo Yuden | JMK325AC7107MM-P | |||
| 100 µF, 6.3V, X5R, 1206, ceramic | Murata | GRM31CR60J107ME39K | ||
| TDK | C3216X5R0J107M | |||
| Würth Electronik | 885012108005 | |||
| LF | 1 | 1 µH, 5.6 mΩ, 16 A, 6.95 × 6.6 × 2.8 mm | Cyntec | CMLE063T-1R0MS |
| 1 µH, 5.5 mΩ, 12 A, 6.65 × 6.45 × 3.0 mm | Würth Electronik | WE XHMI 74439344010 | ||
| 1 µH, 7.9 mΩ, 16 A, 6.5 × 6.0 × 3.0 mm | Panasonic | ETQP3M1R0YFN | ||
| 1 µH, 6.95 mΩ, 18 A, 6.76 × 6.56 × 3.1 mm | Coilcraft | XEL6030-102ME | ||
| Q1 | 1 | 60 V, 8.5 mΩ, high-side MOSFET, SON 3 × 3 | Texas Instruments | CSD18543Q3A |
| Q2 | 1 | 60 V, 4 mΩ, low-side MOSFET, SON 5 × 6 | Texas Instruments | CSD18531Q5A |
| U1 | 1 | Wide VIN synchronous buck controller | Texas Instruments | LM25145RGYR |
| U2 | 1 | 6- or 4-bit VID voltage programmer, WSON-10 | Texas Instruments | LM10011SD |
| U3 | 1 | KeyStone™ DSP | Texas Instruments | TMS320C667x |
The regulator output current requirements are dependent upon the baseline and activity power consumption of the DSP in a real-use case. While baseline power is highly dependent on voltage, temperature and DSP frequency, activity power relates to dynamic core utilization, DDR3 memory access, peripherals, and so on. To this end, the IDAC_OUT pin of the LM10011 connects to the LM25145 FB pin to allow continuous optimization of the core voltage. The SmartReflex-enabled DSP provides 6-bit information using the VCNTL open-drain I/Os to command the output voltage setpoint with 6.4-mV step resolution.(1)
9.2.3.3 Application Curves
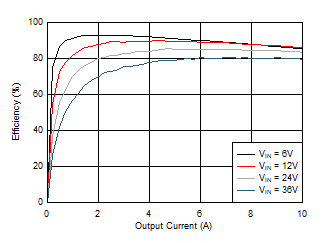
| VOUT = 1.1 V | VAUX = 8 V |

| VIN = 24 V | 0.11-Ω Load |
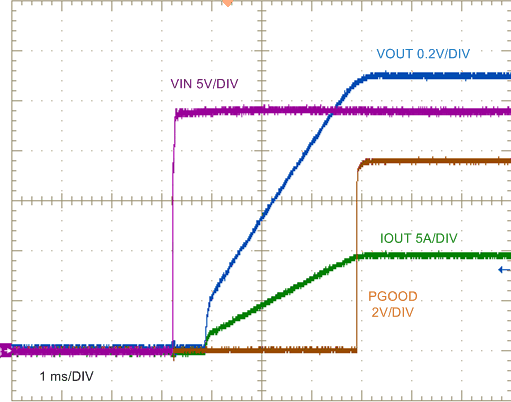
| VIN step to 24 V | 0.11-Ω Load |
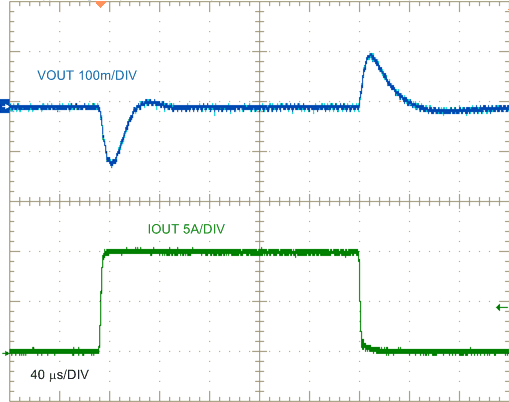
| VIN = 24 V |