SNVSA24 October 2014 LMR16006
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Simplified Schematic
- 5 Revision History
- 6 Pin Configuration and Functions
- 7 Specifications
- 8 Detailed Description
- 9 Application and Implementation
- 10Power Supply Recommendations
- 11Layout
- 12Device and Documentation Support
- 13Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
- DDC|6
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9 Application and Implementation
NOTE
Information in the following applications sections is not part of the TI component specification, and TI does not warrant its accuracy or completeness. TI’s customers are responsible for determining suitability of components for their purposes. Customers should validate and test their design implementation to confirm system functionality.
9.1 Application Information
The LMR16006 is a step down DC-to-DC regulator. It is typically used to convert a higher DC voltage to a lower DC voltage with a maximum output current of 600 mA. The following design procedure can be used to select components for the LMR16006. This section presents a simplified discussion of the design process.
9.2 Typical Application
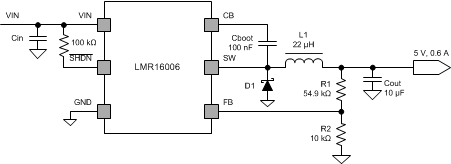 Figure 9. Application Circuit, 5 V Output
Figure 9. Application Circuit, 5 V Output
9.2.1 Design Requirements
Table 1. Design Example Parameters
| Input Voltage, VIN | 9 V to 16 V, Typical 12 V | |
| Output Voltage, VOUT | 5.0 V ± 3% | |
| Maximum Output Current IO_max | 0.6 A | |
| Minimum Output Current IO_min | 0.03 A | |
| Transient Response 0.03 A to 0.6 A | 5% | |
| Output Voltage Ripple | 1% | |
| Switching Frequency Fsw | 0.7 MHz | |
| Target during Load Transient | Over Voltage Peak Value | 106% of Output Voltage |
| Under Voltage Value | 91% of Output Voltage | |
9.2.2 Detailed Design Procedure
9.2.2.1 Custom Design with WEBENCH Tools
Click here to create a custom design using the LMR16006 device with the WEBENCH® Power Designer.
- Start by entering your VIN, VOUT and IOUT requirements.
- Optimize your design for key parameters like efficiency, footprint and cost using the optimizer dial and compare this design with other possible solutions from Texas Instruments.
- WEBENCH Power Designer provides you with a customized schematic along with a list of materials with real time pricing and component availability.
- In most cases, you will also be able to:
- Run electrical simulations to see important waveforms and circuit performance,
- Run thermal simulations to understand the thermal performance of your board,
- Export your customized schematic and layout into popular CAD formats,
- Print PDF reports for the design, and share your design with colleagues.
- Get more information about WEBENCH tools at www.ti.com/webench.
This example details the design of a high frequency switching regulator using ceramic output capacitors. A few parameters must be known in order to start the design process. These parameters are typically determined at the system level:
9.2.2.2 Output Inductor Selection
The most critical parameters for the inductor are the inductance, peak current and the DC resistance. The inductance is related to the peak-to-peak inductor ripple current, the input and the output voltages. Since the ripple current increases with the input voltage, the maximum input voltage is always used to determine the inductance. To calculate the minimum value of the output inductor, use Equation 1. KIND is a coefficient that represents the amount of inductor ripple current relative to the maximum output current. A reasonable value is setting the ripple current to be 30%-40% of the DC output current. For this design example, the minimum inductor value is calculated to be 20.4 µH, and a nearest standard value was chosen: 22 µH. For the output filter inductor, it is important that the RMS current and saturation current ratings not be exceeded. The RMS and peak inductor current can be found from Equation 3 and Equation 4. The inductor ripple current is 0.22 A, and the RMS current is 0.602 A. As the equation set demonstrates, lower ripple currents will reduce the output voltage ripple of the regulator but will require a larger value of inductance. A good starting point for most applications is 22 μH with a 1.6 A current rating. Using a rating near 1.6 A will enable the LMR16006 to current limit without saturating the inductor. This is preferable to the LMR16006 going into thermal shutdown mode and the possibility of damaging the inductor if the output is shorted to ground or other long-term overload.
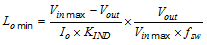
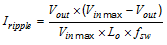
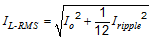
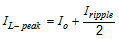
9.2.2.3 Output Capacitor Selection
The selection of Cout is mainly driven by three primary considerations. The output capacitor will determine the modulator pole, the output voltage ripple, and how the regulator responds to a large change in load current. The output capacitance needs to be selected based on the most stringent of these three criteria.
The desired response to a large change in the load current is the first criteria. The regulator usually needs two or more clock cycles for the control loop to see the change in load current and output voltage and adjust the duty cycle to react to the change. The output capacitance must be large enough to supply the difference in current for 2 clock cycles while only allowing a tolerable amount of droop in the output voltage. Equation 5 shows the minimum output capacitance necessary to accomplish this. The transient load response is specified as a 3% change in VOUT for a load step from 0.03 A to 0.6 A (full load), ΔIOUT = 0.6 -0.03 = 0.57 A and ΔVOUT = 0.03 × 5 = 0.15 V. Using these numbers gives a minimum capacitance of 10.8 µF. For ceramic capacitors, the ESR is usually small enough to ignore in this calculation. Aluminum electrolytic and tantalum capacitors have higher ESR that should be taken into account.
The stored energy in the inductor will produce an output voltage overshoot when the load current rapidly decreases. The output capacitor must also be sized to absorb energy stored in the inductor when transitioning from a high load current to a lower load current. Equation 6 is used to calculate the minimum capacitance to keep the output voltage overshoot to a desired value. Where L is the value of the inductor, IOH is the output current under heavy load, IOL is the output under light load, Vf is the final peak output voltage, and Vi is the initial capacitor voltage. For this example, the worst case load step will be from 0.6 A to 0.03 A. The output voltage will increase during this load transition and the stated maximum in our specification is 3% of the output voltage. This will make Vo_overshoot = 1.03 × 5 = 5.15 V. Vi is the initial capacitor voltage which is the nominal output voltage of 5 V. Using these numbers in Equation 6 yields a minimum capacitance of 5.2 µF.
Equation 7 calculates the minimum output capacitance needed to meet the output voltage ripple specification. Where fsw is the switching frequency, Vo_ripple is the maximum allowable output voltage ripple, and IL_ripple is the inductor ripple current. Equation 7 yields 0.26 µF.
Equation 8 calculates the maximum ESR an output capacitor can have to meet the output voltage ripple specification. Equation 8 indicates the ESR should be less than 680 mΩ.
Additional capacitance de-ratings for aging, temperature and dc bias should be factored in which will increase this minimum value. For this example, 10 µF ceramic capacitors will be used. Capacitors in the range of 4.7 µF-100 µF are a good starting point with an ESR of 0.7 Ω or less.
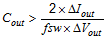
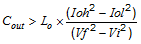
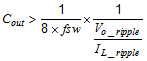
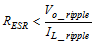
9.2.2.4 Schottky Diode Selection
The breakdown voltage rating of the diode is preferred to be 25% higher than the maximum input voltage. In the target application, the current rating for the diode should be equal or greater to the maximum output current for best reliability in most applications. In cases where the input voltage is not much greater than the output voltage the average diode current is lower. In this case it is possible to use a diode with a lower average current rating, approximately (1-D) × IOUT. However the peak current rating should be higher than the maximum load current. A 0.5 A to 1 A rated diode is a good starting point.
9.2.2.5 Input Capacitor Selection
A low ESR ceramic capacitor is needed between the VIN pin and ground pin. This capacitor prevents large switching voltage transients from appearing at the input. Use a 1 µF-10 µF value with X5R or X7R dielectric. Depending on construction, a ceramic capacitor’s value can decrease up to 50% of its nominal value when rated voltage is applied. Consult with the capacitor manufactures data sheet for information on capacitor derating over voltage and temperature. The capacitor must also have a ripple current rating greater than the maximum input current ripple of the LMR16006. The input ripple current can be calculated using below Equation 9.
For this example design, one 2.2 µF, 50 V capacitor is selected. The input capacitance value determines the input ripple voltage of the regulator. The input voltage ripple can be calculated using Equation 10. Using the design example values, IOUT_max = 0.6 A, Cin = 2.2 µF, ƒSW = 700 kHz, yields an input voltage ripple of 97 mV and a rms input ripple current of 0.3 A.
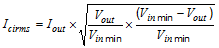
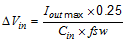
9.2.2.6 Bootstrap Capacitor Selection
A 0.1 μF ceramic capacitor or larger is recommended for the bootstrap capacitor (CBOOT). For applications where the input voltage is close to output voltage a larger capacitor is recommended, generally 0.1 µF to 1 µF to ensure plenty of gate drive for the internal switches and a consistently low RDSON. A ceramic capacitor with an X7R or X5R grade dielectric with a voltage rating of 10 V or higher is recommended because of the stable characteristics over temperature and voltage.
Table 2 represents the recommended typical output voltage inductor/capacitor combinations for optimized total solution size.
Table 2. Recommended Typical Output Voltage
| P/N | Vout (V) | R1 (kΩ) | R2 (kΩ) | L (μH) | Cout (μF) |
|---|---|---|---|---|---|
| LMR16006 Y | 5 | 54.9 (1%) | 10 (1%) | 6.8 | 10 |
| LMR16006 Y | 12 | 147 (1%) | 10 (1%) | 10 | 10 |
9.2.3 Application Curves
Unless otherwise specified the following conditions apply: VIN = 12 V, fSW = 700 kHz, L1 = 22 µH, Cout = 10 µF, TA = 25°C
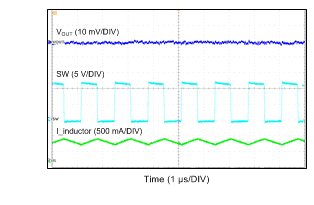
| VOUT = 5 V | IOUT = 600 mA | |
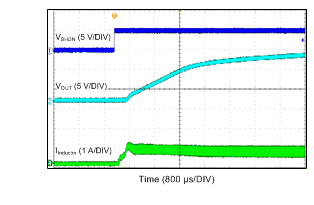
| VIN = 24 V | VOUT = 12 V | IOUT = 600 mA |
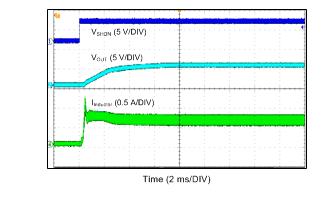
| VIN = 12 V | VOUT = 5 V | IOUT = 600 mA |
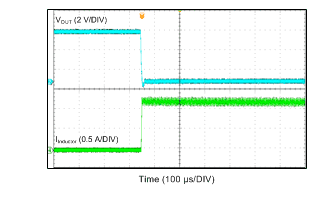
| VIN = 12 V | VOUT = 5 V | |
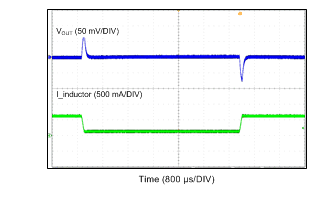
| VOUT = 5 V | ||
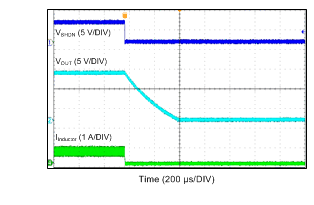
| VIN = 24 V | VOUT = 12 V | IOUT = 600 mA |
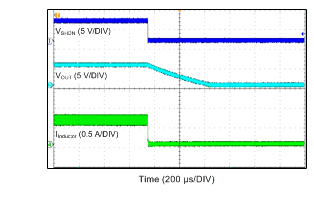
| VIN = 12 V | VOUT = 5 V | IOUT = 600 mA |
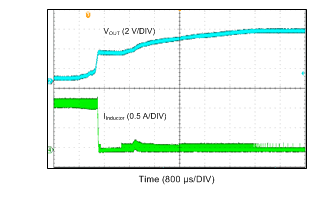
| VIN = 12 V | VOUT = 5 V | |