SBAA399 February 2023 ADS7028 , ADS7128
1 TI Tech Note
Overview
The root-mean-square (RMS) value of an AC voltage waveform signifies the effective voltage across a load, that is, the RMS is equal to the DC voltage that can deliver the same power to a load. The RMS value is used to asses the power quality of an AC supply. There are two popular methods of computing RMS, the Averaging RMS and True RMS methods. The True RMS method is a superset technique that can be used for non-periodic signals, which includes both linear and non-linear loads. This technique is required in electrical grid applications due to the occurrence of sinusoidal and non-sinusoidal voltages and currents in the system. Thus, electrical measuring instruments used for such assessment need to be able to compute RMS of AC signals. This document focuses on the performance of the True RMS module integrated into the ADS7x28 family of ADC devices.
What is True RMS?
The RMS of any signal is the square root of the average of the square of any signal as expressed by Equation 1.
where
- T = time period of the signal
- V = instantaneous voltage of the signal
- t = time
True RMS is a method capable of computing the RMS of sinusoidal signals as well as non-sinusoidal signals. A True RMS measuring circuit first squares the input signal, then performs the average of the result over time. This is followed then by completing the square root of the average to finally compute an accurate RMS value of the input signal.
Observation Window
An observation window is the time in which the True RMS measurement detects the input signal to compute the result. To accurately calculate True RMS, the observation window must include an integer number of half cycles of the input signal. Figure 1-1 shows an example of a sinusoidal signal with an integer number of 2 half cycles within the observation window. If the observation window does not include an integer number of half cycles, as shown in Figure 1-2, the True RMS computation is not accurate.
The observation window requires a sufficient number of half cycles to accurately compute the True RMS, though one half-cycle results in a True RMS value. Include a minimum of 32 half cycles to achieve a true RMS with less than 0.5% error. Generally, as the frequency of input signal increases, more cycles are observed within the same observation window which results in a decreasing RMS error.
ADS7x28 RMS Module
ADS7x28 is an 8-channel, 12-bit SAR ADC with an integrated True RMS module. Any one analog input channel can be selected for computing the RMS result. The ADS7x28 observation window used for the True RMS computation can be configured within the device using Equation 2:
where
- RMS_SAMPLES is the total number of samples used to calculate the RMS value
- ƒCYCLE is the sample rate of the ADC
Based on the recommendation of a minimum of 32 half cycles of the input signal within the observation window, Table 1-1 lists the recommended observation window with regard to the input signal frequency, and the ADS7x28 configuration to achieve the observation window.
| Input Signal Frequency Cutoff |
RMS_SAMPLES | ƒCYCLE | Minimum
Observation Window |
|---|---|---|---|
| ≤ 80 Hz | 65536 | 333.3 kSPS | 200 ms |
| ≤ 40 Hz | 65536 | 166.7 kSPS | 400 ms |
| ≤ 20 Hz | 65536 | 83 kSPS | 800 ms |
| ≤ 10 Hz | 65536 | 41.7 kSPS | 1600 ms |
| ≤5 Hz | 65536 | 20.8 kSPS | 3200 ms |
RMS of AC Only
The ADS7x28 features the capability of completing the RMS of only the AC component by subtracting the DC input signal component in the True RMS measurement. If True RMS of only the AC component of the input signal is desired, DC subtraction can be enabled by following the configuration setting of the DC_SUB register of the device as shown in Table 1-2.
| True RMS Measurement | DC_SUB Register |
|---|---|
| AC + DC | 0b |
| AC only | 1b |
The device implements Equation 3 when the AC only input signal component is selected.
Figure 1-3 shows the uncalibrated RMS measurement percent error vs input voltage, this means the setting AC only was used.
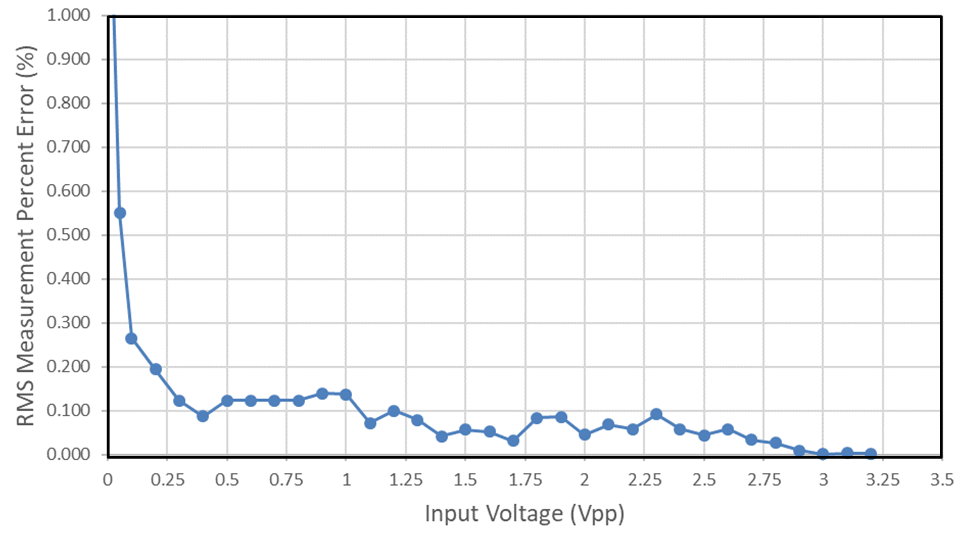 Figure 1-3 AC Only Percentage
Error
Figure 1-3 AC Only Percentage
ErrorImproving AC Only RMS Results
Implementing a calibration to the RMS calculated can improve the RMS result when using AC only using Equation 4.
Steps for calibration:
- Connect unipolar input signal to one channel of ADS7x28
- Connect the DC offset to another channel
- Compute AC only RMS of the channel with input signal (ACRMS)
- Compute AC only RMS of the channel with only DC offset applied (DCRMS)
- Use Equation 4 to solve for the Calibrated RMS value
Figure 1-4 shows the RMS percent error after calibration plotted against peak-to-peak voltage of the input signal. Calibrating the RMS result reduces the magnitude of RMS error.
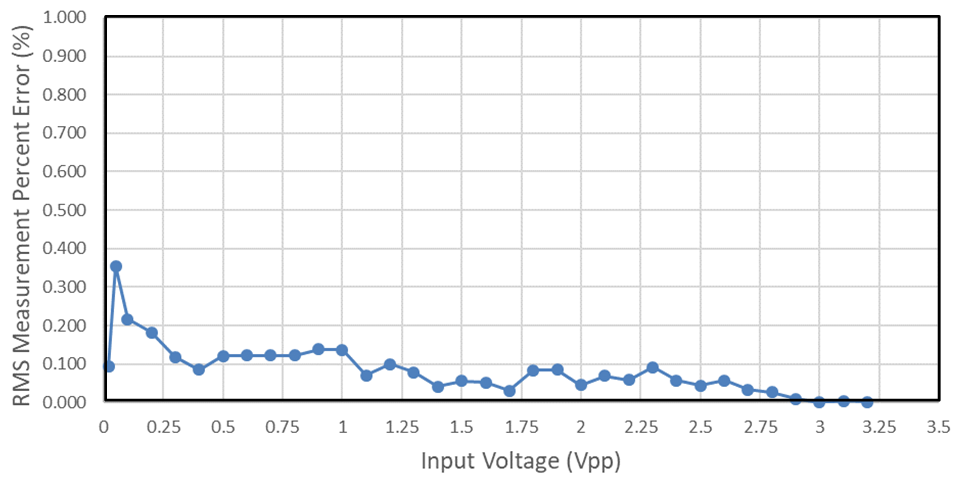 Figure 1-4 ADS7128 RMS Measurement
Percent Error vs Input Voltage (Calibrated)
Figure 1-4 ADS7128 RMS Measurement
Percent Error vs Input Voltage (Calibrated)Conclusion
This brief detailed the merits of RMS computation using ADS7x28 devices.
- Settings through software: Select settings through software. No hardware changes required.
- Simplicity: Only observation window needs to be selected based on the range of input signal frequency through simple software settings. Frequency can be measured by built-in zero crossing detector module. Computation time does not change with crest factor, input signal waveform, amplitude of input signal, and so forth.
- Calibration: Error can be improved by calibration using a simple equation.
- Compact design size: One-chip design
- Low power requirement
- Unipolar supply