Design Description

The Butterworth Sallen-Key (SK) high-pass (HP) filter is a 2nd-order active filter. Vref provides a DC offset to accommodate for single-supply applications.

An SK filter is usually preferred when small Q factor is desired, noise rejection is prioritized, and when a non-inverting gain of the filter stage is required. The Butterworth topology provides a maximally flat gain in the pass band.

Design Notes

1. Select an op amp with sufficient input common-mode range and output voltage swing.
2. Add V_ref to bias the input signal to meet the input common-mode range and output voltage swing.
3. Select the capacitor values first since standard capacitor values are more coarsely subdivided than the resistor values. Use high-precision, low-drift capacitor values to avoid errors in f_c.
4. To minimize the amount of slew-induced distortion, select an op amp with sufficient slew rate (SR).
5. For HP filters, the maximum frequency is set by the gain bandwidth (GBW) of the op amp. Therefore, be sure to select an op amp with sufficient GBW.

Design Steps

The first step is to find component values for the normalized cutoff frequency of 1 radian/second. In the second step the cutoff frequency is scaled to the desired cutoff frequency with scaled component values.

The transfer function for the second-order Sallen-Key high-pass filter is given by:

where,

1. Set normalized values of C₁ and C₂ (C_1n and C_2n) and calculate normalized values of R₁ and R₂ (R_1n and R_2n) by setting w_c to 1 radian/sec (or fc = 1 / (2 × π) Hz). For the second-order Butterworth filter, (see the Butterworth Filter Table in the Active Low-Pass Filter Design Application Report).
   ${\text{a}}_0=\text{1,} {\mathrm{a}}_1=\sqrt{2}\text{,} \text{let }{\mathrm{C}}_{\mathrm{1n}}=C_{\mathrm{2n}}=1 \mathrm{F,} \mathrm{then }{R}_{\mathrm{1n}}\times R_{\mathrm{2n}}=1 \mathrm{or} R_{\mathrm{2n}}=\frac{1}{R_{\mathrm{1n}}}\mathrm{,} a_1=\frac{2}{R_{\mathrm{2n}}}=\sqrt{2}$
   ${\text{∴ R}}_{\mathrm{2n}}=\sqrt{2}=\; 1.414\Omega , R_{\mathrm{1n}}=\frac{1}{R_{\mathrm{2n}}}=\; 0.707\Omega$
2. Scale the component values and cutoff frequency. The resistor values are very small and capacitors values are unrealistic, hence these have to be scaled. The cutoff frequency is scaled from 1 radian/sec to w₀. If m is assumed to be the scaling factor, increase the resistors by m times, then the capacitor values have to decrease by 1/m times to keep the same cutoff frequency of 1 radian/sec. If the cutoff frequency is scaled to be w₀, then the capacitor values have to be decreased by 1 / w₀. The component values for the design goals are calculated in steps 3 and 4.
   ${\text{R}}_1={\text{R}}_{\mathrm{1n}}\times m\text{,} {\text{R}}_2={\text{R}}_{\mathrm{2n}}\times m$
   ${\text{C}}_1=C_2=\frac{C_{\mathrm{1n}}}{m\times w_0}F$
3. Set C₁ and C₂ to 10nF, then calculate m.
   ${\text{w}}_0=2\times \pi \times \text{1kHz,} m=\text{15915.5}$
4. Select R₁ and R₂ based on m.
   ${\text{R}}_{\text{1}}\text{= 0.707 × 15915 = 11252Ω ≈ 11kΩ (Standard Value)}$
   ${\text{R}}_{\text{2}}\text{= 1.414 × 15915 = 22504Ω ≈ 23kΩ (Standard Value)}$
5. Calculate the minimum required GBW and SR for f_max.
   ${\text{GBW = 100 × Gain × f}}_{\text{max}}\text{ = 100 × 1 × 10kHz = 1MHz}$
   ${\text{SR = 2 × π × f}}_{\max }{\text{ × V}}_{\mathrm{ipeak}}\text{ = 2 × π × 10kHz × 2.45V = 0.154}\frac{V}{\mathrm{\mu s}}$

   The TLV9062 device has a GBW of 10MHz and SR of 6.5V/µs, so it meets these requirements.

Design Simulations

AC Simulation Results

Transient Simulation Results

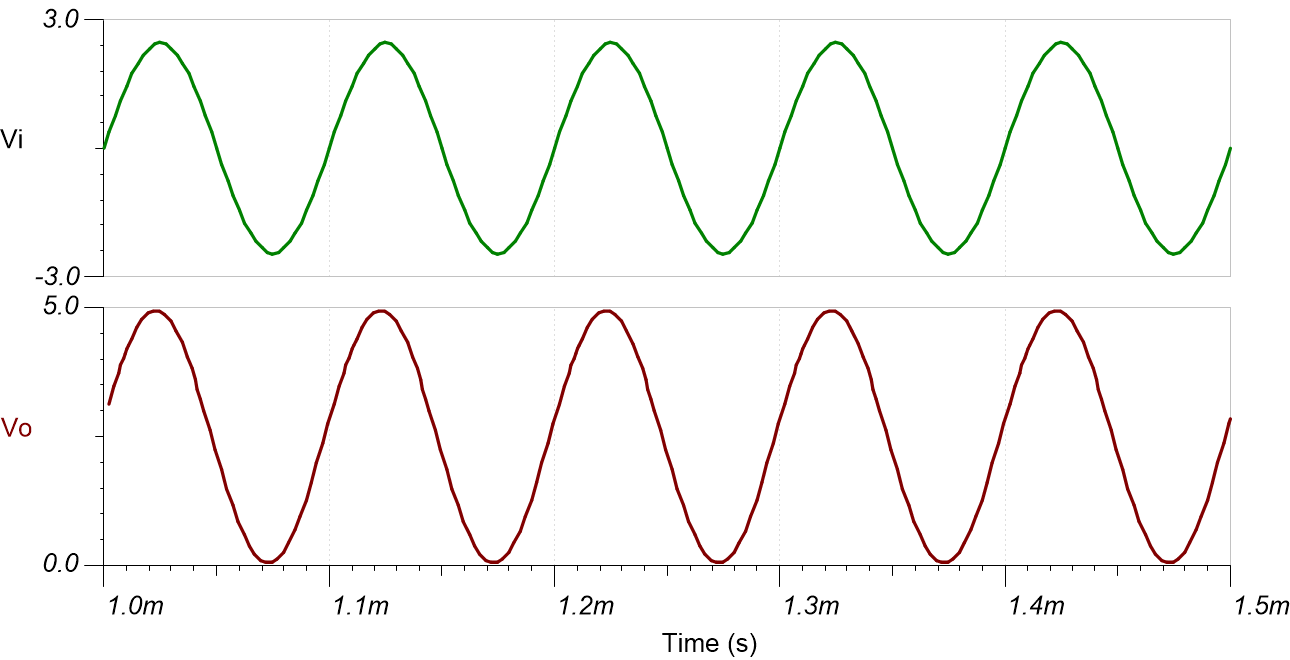
The following image shows the filter output in response to a ± 2.5-V, 10-kHz input signal (gain is 1V / V).

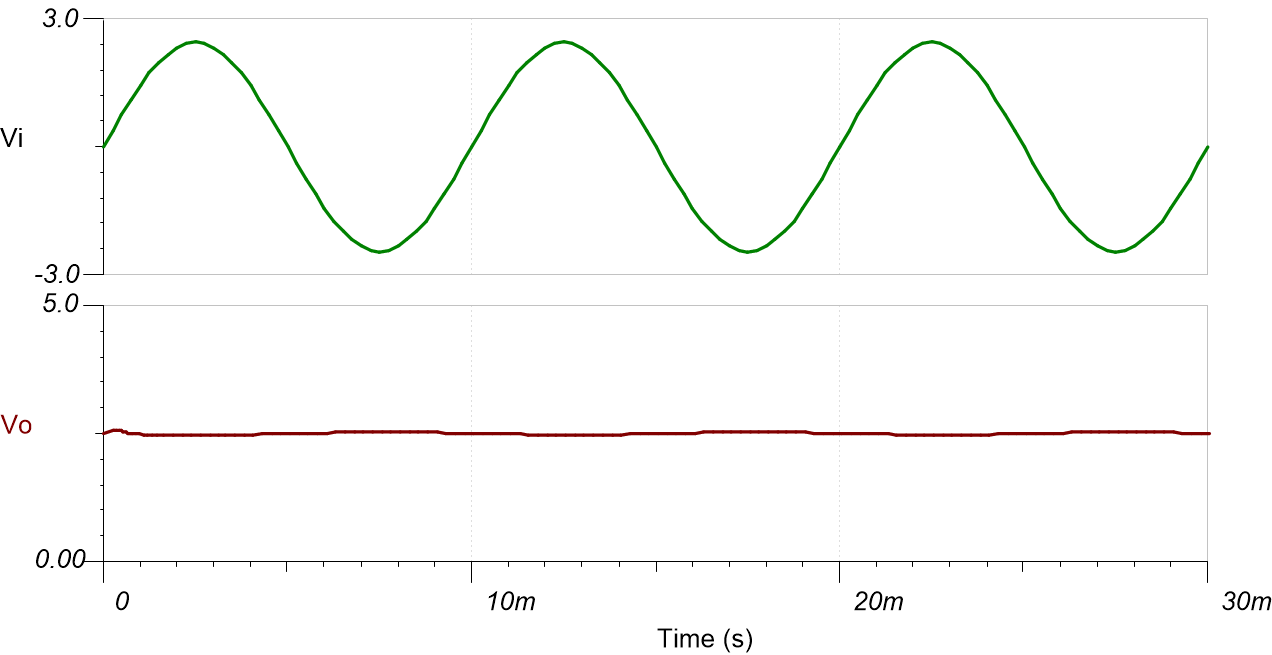
The following image shows the filter output in response to a ± 2.5-V, 10-Hz input signal (gain is 0.014V / V).

Design References

1. See Analog Engineer's Circuit Cookbooks for TI's comprehensive circuit library.
2. SPICE Simulation File - SBOMB38.
3. TI Precision Labs

Design Featured Op Amp

Design Alternate Op Amp