SBOA231 June 2021 OPA325 , TLV316 , TLV9062
| Input | Output | Supply | |||
|---|---|---|---|---|---|
| ViMin | ViMax | VoMin | VoMax | Vcc | Vee |
| –2.45V | +2.45V | 0.05V | 4.95V | 5V | 0V |
| Gain | Cutoff Frequency (fc) | Vref |
|---|---|---|
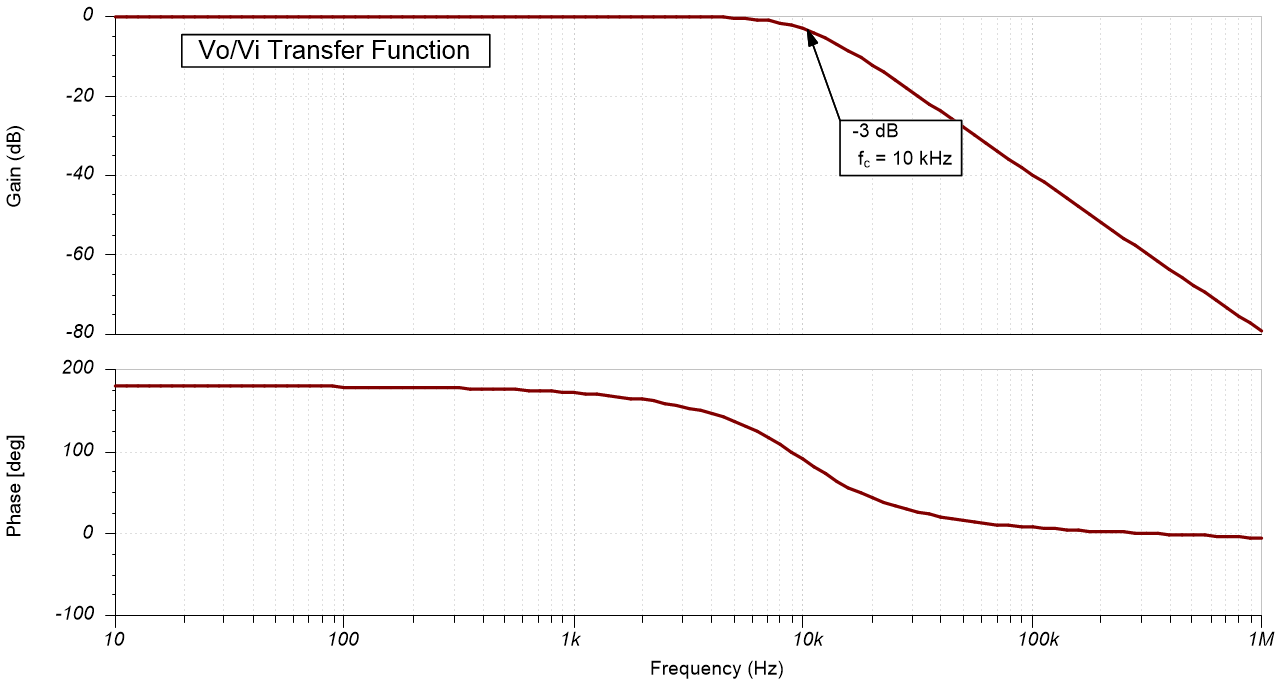
| –1V/V | 10kHz | 1.25V |
Design Description
The multiple-feedback (MFB) low-pass filter (LP filter) is a second-order active filter. Vref provides a DC offset to accommodate for single-supply applications. This LP filter inverts the signal (Gain = –1V/V) for frequencies in the pass band. An MFB filter is preferable when the gain is high or when the Q-factor is large (for example, 3 or greater).

Design Notes
- Select an op amp with sufficient input common-mode range and output voltage swing.
- Add Vref to bias the input signal to meet the input common-mode range and output voltage swing.
- Select the capacitor values first since standard capacitor values are more coarsely subdivided than the resistor values. Use high-precision, low-drift capacitor values to avoid errors in fc.
- To minimize the amount of slew-induced distortion, select an op amp with sufficient slew rate (SR).
Design Steps
The first step in design is to find component values for the normalized cutoff frequency of 1 radian/second. In the second step the cutoff frequency is scaled to the desired cutoff frequency with scaled component values.
The transfer function for a second-order MFB low-pass filter is given by:
- Set normalized values of
R1 and R2 (R1n and R2n) and
calculate normalized values of C1 and C2 (C1n
and C2n) by setting wc to 1 radian/sec (or fc = 1 / (2 ×
π) Hz). For a 2nd-order Butterworth filter, (see the Butterworth Filter
Table in the Active Low-Pass Filter Design Application
Report).
- Scale the component values and
cutoff frequency. The resistor values are very small and capacitors values are
unrealistic, hence these must be scaled. The cutoff frequency is scaled from 1
radian/second to w0. If m is assumed to be the scaling factor,
increase the resistors by m times, then the capacitor values have to
decrease by 1/m times to keep the same cutoff frequency of 1
radian/second. If the cutoff frequency is scaled to be w0, then the
capacitor values have to be decreased by 1/wo. The component values
for the design goals are calculated in steps 3 and 4.
- Set R1, R2,
and R3 to 10kΩ.
- Calculate
C1 and C2 based on m and w0.
- Calculate the minimum required GBW
and SR for fc. Be sure to use the noise gain for GBW calculations. Do
not use the signal gain of –1V/V.
The TLV9062 device has GBW of 10MHz and SR of 6.5 V/µs, so the requirements are met.
Design Simulations
AC Simulation Results
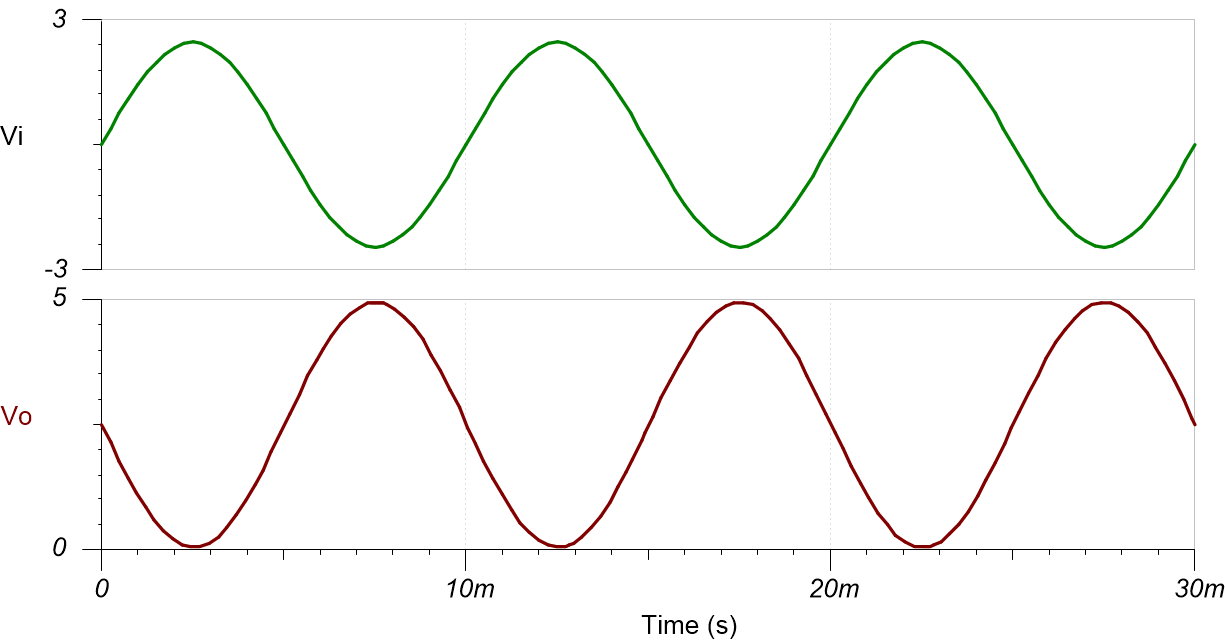
Transient Simulation Results
The following image shows the filter output in response to a 5-Vpp, 100-Hz input signal (gain = –1V/V).
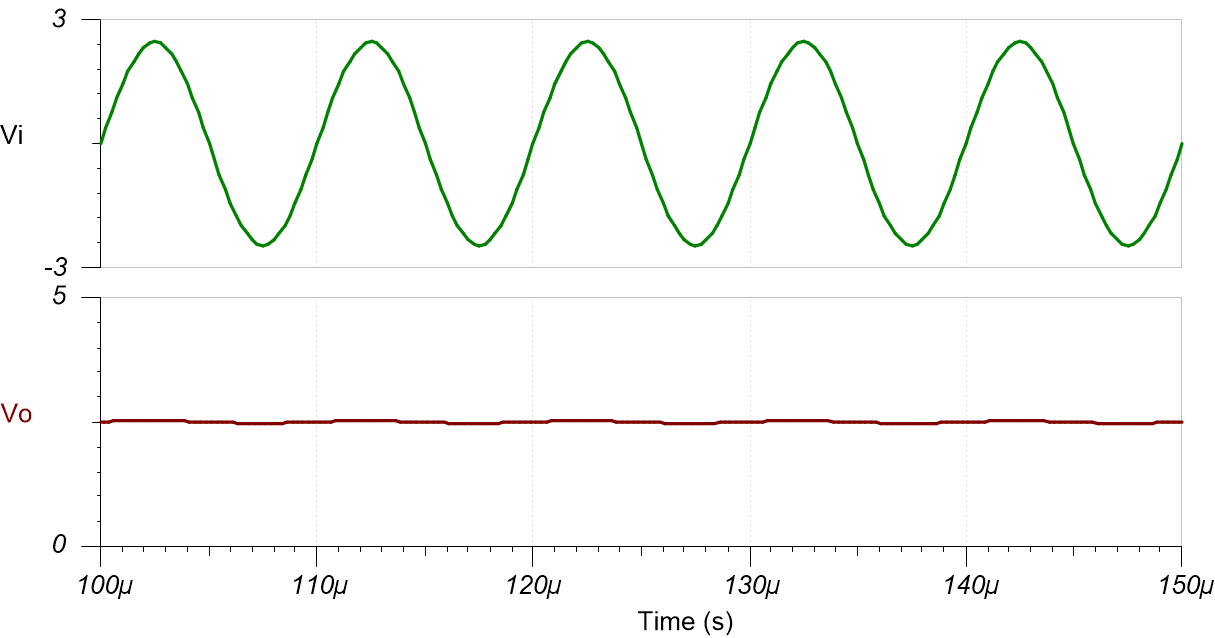
The following image shows the filter output in response to a 5-Vpp, 10-kHz input signal (gain = –0.01V/V).
Design References
- See Analog Engineer's Circuit Cookbooks for TI's comprehensive circuit library.
- SPICE Simulation File SBOC597
- TI Precision Labs.
- Active Low-Pass Filter Design Application Report
Design Featured Op Amp
| TLV9062 | |
|---|---|
| Vss | 1.8V to 5.5V |
| VinCM | Rail-to-Rail |
| Vout | Rail-to-Rail |
| Vos | 0.3mV |
| Iq | 538µA |
| Ib | 0.5pA |
| UGBW | 10MHz |
| SR | 6.5V/µs |
| #Channels | 1, 2, 4 |
| www.ti.com/product/TLV9062 | |
Design Alternate Op Amp
| TLV316 | OPA325 | |
|---|---|---|
| Vss | 1.8V to 5.5V | 2.2V to 5.5V |
| VinCM | Rail-to-Rail | Rail-to-Rail |
| Vout | Rail-to-Rail | Rail-to-Rail |
| Vos | 0.75mV | 0.150mV |
| Iq | 400µA | 650µA |
| Ib | 10pA | 0.2pA |
| UGBW | 10MHz | 10MHz |
| SR | 6V/µs | 5V/µs |
| #Channels | 1, 2, 4 | 1, 2, 4 |
| www.ti.com/product/TLV316 | www.ti.com/product/OPA325 |