SLVAFJ5 Application brief

Part 2 of this topology series discusses how to choose the best-fitting topology from the parameters of the power-supply specification. This application brief describes different in-depth aspects for buck, boost, and buck-boost topologies.

Buck Converters

Figure 1-1 shows the schematic of a nonsynchronous buck converter. A buck converter steps down the input voltage to a lower output voltage. The energy transfers to the output when switch Q1 is conducting.

Figure 1-1 Nonsynchronous Buck Converter Schematic

Equation 1 calculates the duty cycle as:

Equation 1.

D = \frac{V_{O U T} + V_{f}}{V_{I N} + V_{f}}

Equation 2 calculates the maximum metal-oxide semiconductor field-effect transistor (MOSFET) stress as:

Equation 2.

V_{Q 1} = V_{I N} + V_{f}

Equation 3 gives the maximum diode stress as:

Equation 3.

V_{D 1} = V_{I N}

where

V_IN is the input voltage
V_OUT is the output voltage
V_ƒ is the diode forward voltage

The bigger the difference between the input voltage and output voltage, the greater the efficiency of the buck converter compared to a linear regulator or low-dropout regulator (LDO).

While a buck converter has a pulsed current at the input, the output current is continuous due to the inductor-capacitor (LC) filter located at the output of the converter. As a result, the voltage ripple reflected to the input is larger compared to the ripple at the output.

For buck converters with a small duty cycle and output currents greater than 3 A, use a synchronous rectifier. If the power supply requires output currents greater than 30 A, use a multiphase or interleaved power stage, because this minimizes the stress for components, spreads the generated heat among multiple power stages, and reduces the reflected ripple at the input of the converter.

Duty-cycle limitations can occur when using an N-FET, because the bootstrap capacitor needs to be recharged every switching cycle. In this case, the maximum duty cycle is in the range of 95%–99%.

Buck converters generally have good dynamic behavior because these converters represent a forward topology. The achievable bandwidth depends on the quality of the error amplifier and the chosen switching frequency.

Figure 1-2 through Figure 1-7 show voltage and current waveforms in continuous conduction mode (CCM) for the FET, diode and inductor in a nonsynchronous buck converter.

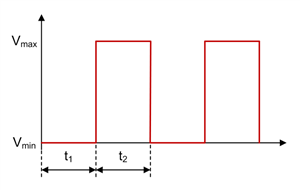
Figure 1-2 Buck FET Voltage Waveform in CCM

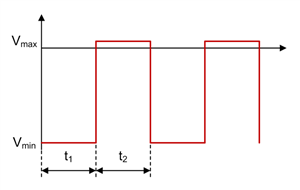
Figure 1-4 Buck Diode Voltage Waveform in CCM

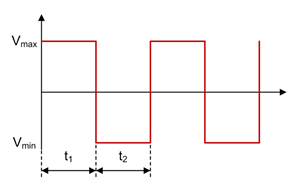
Figure 1-6 Buck Inductor Voltage Waveform in CCM

Figure 1-3 Buck FET Current Waveform in CCM

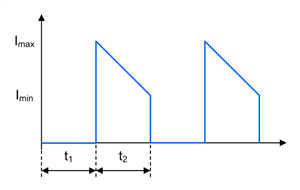
Figure 1-5 Buck Diode Current Waveform in CCM

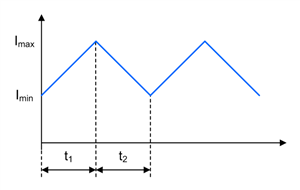
Figure 1-7 Buck Inductor Current Waveform in CCM

Boost Converters

A boost converter steps up the input voltage to a larger output voltage. The energy transfers to the output when switch Q1 is not conducting. Figure 1-8 is a schematic of a nonsynchronous boost converter.

Figure 1-8 Nonsynchronous Boost Converter Schematic

Equation 4 calculates the duty cycle as:

Equation 4.

D = \frac{V_{O U T} + V_{f} - V_{I N}}{V_{O U T} + V_{f}}

Equation 5 calculates the maximum MOSFET stress as:

Equation 5.

V_{Q 1} = V_{O U T} + V_{f}

Equation 6 gives the maximum diode stress as:

Equation 6.

V_{D 1} = V_{O U T}

where

V_IN is the input voltage
V_OUT is the output voltage
V_f is the diode forward voltage

With a boost converter, a pulsed output current is visible, because the LC filter is located at the input. Thus, the input current is continuous and the output voltage ripple is larger than the input voltage ripple.

When designing a boost converter, it is important to know that there is a permanent connection from the input to the output, even when the converter is not switching. Take precautions in case of a possible short event at the output.

For output currents greater than 4 A, replace the diode with a synchronous rectifier. In case the power-supply needs to provide output currents greater than 10 A, a multiphase or interleaved power-stage approach is recommended.

When operating in CCM, the dynamic behavior of a boost converter is limited due to the right half-plane zero (RHPZ) of the transfer function. Because the RHPZ cannot be compensated, the achievable bandwidth is usually less than one-fifth to one-tenth the RHPZ frequency. See Equation 7:

Equation 7.

f_{R H P Z} = \frac{V_{O U T} \times {(1 - D)}^{2}}{2 \times π \times L_{1} \times I_{O U T}}

where

V_OUT is the output voltage
D is the duty cycle
I_OUT is the output current
L₁ is the inductance of the boost converter

Figure 1-9 through Figure 1-14 show the voltage and current waveforms in CCM for the FET, diode and inductor in a nonsynchronous boost converter.

Figure 1-9 Boost FET Voltage Waveform in CCM

Figure 1-11 Boost Diode Voltage Waveform in CCM

Figure 1-13 Boost Inductor Voltage Waveform in CCM

Figure 1-10 Boost FET Current Waveform in CCM

Figure 1-12 Boost Diode Current Waveform in CCM

Figure 1-14 Boost Inductor Current Waveform in CCM

Buck-Boost Converters

A buck-boost converter is a combination of a buck and a boost power stage, which share the same inductor (see Figure 1-15).

Figure 1-15 Two-Switch Buck-Boost Converter Schematic

The buck-boost topology is useful because the input voltage can be smaller, greater, or equal to the output voltage, while the output power needed is bigger than 50 W.

For an output power smaller than 50 W, a single-ended primary inductance converter (SEPIC) is a more cost-effective choice because this converter uses less components.

A buck-boost converter operates in buck mode when the input voltage is greater than the output voltage, and in boost mode for input voltages smaller than the output voltage. When the converter is operating in the transfer region, which is when the input voltage is in the range of the output voltage, there are two concepts for handling these conditions: either both the buck and boost stage are active at the same time, or the switching cycles alternate between the buck and boost stages, each usually running at half the regular switching frequency. The second concept can cause subharmonic noise at the output and the output-voltage precision can be a little bit less accurate compared to regular buck or boost operation, but the converter is much more efficient compared to the first concept.

The buck-boost topology has pulsed currents at the input and the output, as there is no LC filter pointing in either direction.

You can use the buck and boost power-stage calculations, respectively, for a buck-boost converter.

Buck-boost converters with two switches are designed for a power range between 50 W and 100 W (such as the LM5118), with synchronous rectification up to 400 W possible (as with the LM5175). Using synchronous rectifiers with the same current limits as for the uncombined buck and boost power stages is recommended.

Design the compensation network of a buck-boost converter for the boost stage, because the RHPZ is the limiting factor of the bandwidth of the regulator.

Part 4 discusses the features and drawbacks of the SEPIC and Zeta converter.

Additional Resources

Watch these TI training videos: