SLVAFJ6 March 2023
This application brief introduces the single-ended primary inductance converter (SEPIC) and Zeta converter. Both topologies can be a cost-effective alternative to a buck-boost converter in the power range up to 25 W.
SEPICs
The SEPIC topology can step up and step down the input voltage. The energy transfers from the input to the output when switch Q1 is not conducting. Figure 1-1 shows the schematic of a nonsynchronous SEPIC.
Figure 1-1 Nonsynchronous SEPIC Schematic
Equation 1 calculates the duty cycle in continuous conduction mode (CCM) as:
Equation 2 calculates the maximum metal-oxide semiconductor field-effect transistor (MOSFET) stress as:
Equation 3 gives the maximum diode stress as:
where
- VIN is the input voltage
- VOUT is the output voltage
- Vƒ is the diode forward voltage
- VC1,ripple is the voltage ripple across the coupling capacitor
The inductor-capacitor (LC) filter L1 and Ci is pointing to the input of the SEPIC. This leads to a smaller ripple at the input due to the continuous current flow. At the output, the ripple is bigger because there is a pulsed output current.
A nonsynchronous SEPIC costs less than a buck-boost topology because only one gate driver (compared to two for a two-switch buck-boost converter) and only two semiconductor components (instead of four) is needed. Another advantage of a SEPIC over a buck-boost topology is the better electromagnetic interference (EMI) behavior when both converters are operating in buck mode as a result of the continuous input current of the SEPIC.
A SEPIC is easily built by using a boost controller because MOSFET Q1 needs to be driven on the low side.
The right half-plane zero (RHPZ) is the limiting factor for the achievable regulation bandwidth of a SEPIC. The maximum bandwidth is roughly one-fifth the RHPZ frequency. Equation 4 calculates an estimation of the single RHPZ frequency of the transfer function of the SEPIC:
Solving Equation 5 for s has either one or two more RHPZs as a result:
where
- VOUT is the output voltage
- D is the duty cycle
- IOUT is the output current
- L1 is the inductance of inductor L1
- L2 is the inductance of inductor L2
- C1 is the capacitance of coupling capacitor C1 and s is the complex frequency variable
Figure 1-2 through Figure 1-11 show voltage and current waveforms in CCM for FET Q1, inductor L1, coupling capacitor C1, diode D1, and inductor L2 in a nonsynchronous SEPIC.
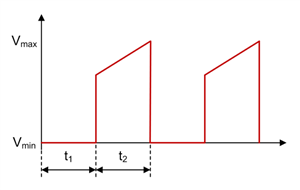
Figure 1-2 SEPIC FET Q1 Voltage Waveform in CCM
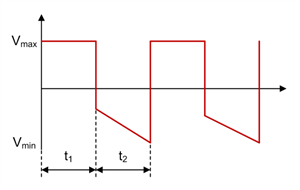
Figure 1-4 SEPIC Inductor L1 Voltage Waveform in CCM
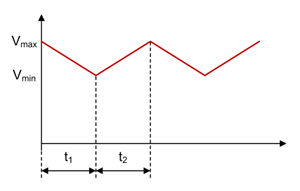
Figure 1-6 SEPIC Coupling Capacitor C1 Voltage Waveform in CCM
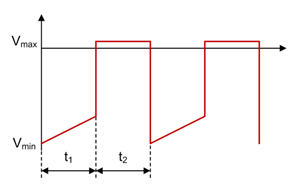
Figure 1-8 SEPIC Diode D1 Voltage Waveform in CCM
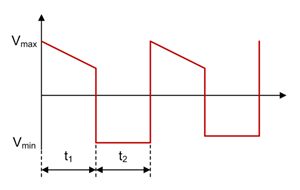
Figure 1-10 SEPIC Inductor L2 Voltage Waveform in CCM
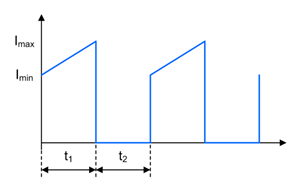
Figure 1-3 SEPIC FET Q1 Current Waveform in CCM
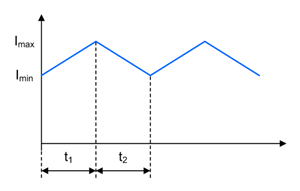
Figure 1-5 SEPIC Inductor L1 Current Waveform in CCM
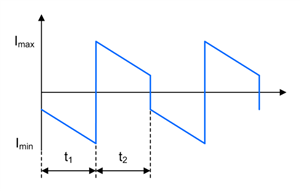
Figure 1-7 SEPIC Coupling Capacitor C1 Current Waveform in CCM
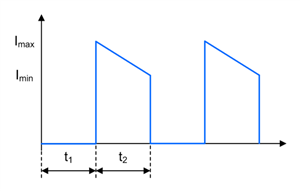
Figure 1-9 SEPIC Diode D1 Current Waveform in CCM
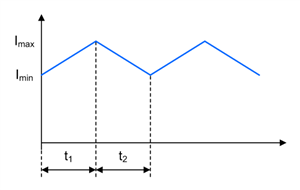
Figure 1-11 SEPIC Inductor L2 Current Waveform in CCM
Zeta Converters
The Zeta topology can step up and step down the input voltage. The energy transfers from the input to the output when switch Q1 is conducting. Figure 1-12 shows the schematic of a nonsynchronous Zeta converter.
Figure 1-12 Nonsynchronous Zeta Converter Schematic
Equation 6 calculates the duty cycle in CCM as:
Equation 7 calculates the maximum MOSFET stress as:
Equation 8 gives the maximum diode stress as:
where
- VIN is the input voltage
- VOUT is the output voltage
- Vƒ is the diode forward voltage
- VC1,ripple is the voltage ripple across the coupling capacitor
The LC filter L2 and Co in a Zeta converter is pointing to the output. As a result, the output ripple is smaller compared to the input ripple, because the output current is continuous and the input current is pulsed. Using the Zeta topology for very sensitive loads is recommended, where a SEPIC or buck-boost converter does not fit due to their higher output ripple. The Zeta topology has the same advantage regarding cost and component count over the buck-boost converter as the SEPIC.
A Zeta converter can be built by using a buck controller or converter; a P-channel MOSFET or high-side MOSFET driver is needed.
The Zeta converter does not have a RHPZ, because the controller can immediately react to changes at the output. Therefore, higher bandwidths with a Zeta converter can be achieved than with a SEPIC or buck-boost converter while using less output capacitance.
Figure 1-13 through Figure 1-22 show voltage and current waveforms in CCM for FET Q1, inductor L1, coupling capacitor C1, diode D1, and inductor L2 in a nonsynchronous Zeta converter.
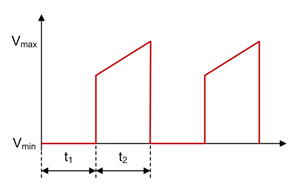
Figure 1-13 Zeta FET Q1 Voltage Waveform in CCM

Figure 1-15 Zeta Inductor L1 Voltage Waveform in CCM
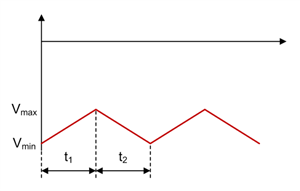
Figure 1-17 Zeta Coupling Capacitor C1 Voltage Waveform in CCM
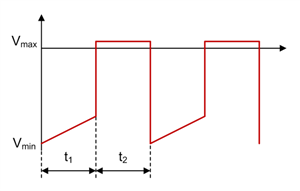
Figure 1-19 Zeta Diode D1 Voltage Waveform in CCM
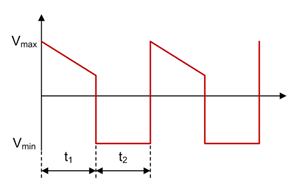
Figure 1-21 Zeta Inductor L2 Voltage Waveform in CCM
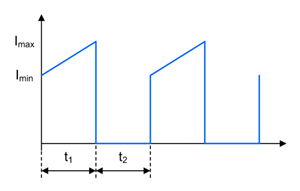
Figure 1-14 Zeta FET Q1 Current Waveform in CCM
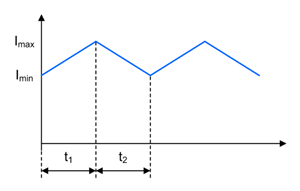
Figure 1-16 Zeta Inductor L1 Current Waveform in CCM
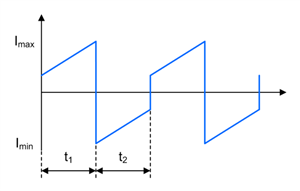
Figure 1-18 Zeta Coupling Capacitor C1 Current Waveform in CCM
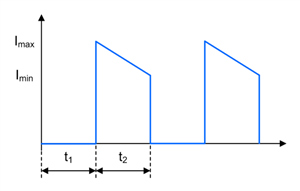
Figure 1-20 Zeta Diode D1 Current Waveform in CCM
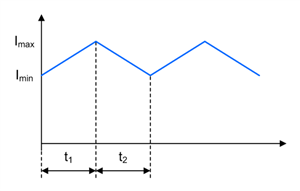
Figure 1-22 Zeta Inductor L2 Current Waveform in CCM
For both topologies, using coupled inductors instead of two separate inductors has two advantages. The first advantage is that only half the inductance is required for a similar current ripple (compared to a two-inductor design) because of ripple cancellation by coupling the windings. The second advantage is that the resonance in the transfer function caused by the two inductors and the coupling capacitor can be removed. Dampen this resonance with a resistor-capacitor (RC) network in parallel with coupling capacitor C1, if needed.
One drawback to using coupled inductors is that the same inductance value for both inductors must be used. Another limitation is typically their current rating. Single inductors can sometimes be needed for applications with high output currents.
It is possible to configure both topologies as a converter with synchronous rectification. But if this method is used, you must AC-couple the high-side gate-drive signal, because many controllers require that you connect them to the switch node. Both topologies have two switch nodes each, so take care to avoid negative voltage-rating violations on the switch pin. Two examples with a synchronous SEPIC and a synchronous Zeta converter are the 12V@5A Synchronous SEPIC Converter Reference Design and the 40W Synchronous Zeta Converter with Two Inductors Reference Design, respectively.
Additional Resources
- Watch these TI training videos:
- Read these Analog Applications Journal articles:
- Design your power stage with Power Stage Designer.
- Download the Power Topologies Handbook and Power Topologies Quick Reference Guide.