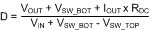SNVS579L February 2009 – May 2018 LM26420
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Pin Configuration and Functions
- 6 Specifications
- 7 Detailed Description
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Applications
- 8.2.1 LM26420X 2.2-MHz, 0.8-V Typical High-Efficiency Application Circuit
- 8.2.2 LM26420X 2.2-MHz, 1.8-V Typical High-Efficiency Application Circuit
- 8.2.3 LM26420X 2.2-MHz, 2.5-V Typical High-Efficiency Application Circuit
- 8.2.4 LM26420Y 550 kHz, 0.8-V Typical High-Efficiency Application Circuit
- 8.2.5 LM26420Y 550-kHz, 1.8-V Typical High-Efficiency Application Circuit
- 8.2.6 LM26420Y 550-kHz, 2.5-V Typical High-Efficiency Application Circuit
- 9 Power Supply Recommendations
- 10Layout
- 11Device and Documentation Support
- 12Mechanical, Packaging, and Orderable Information
8.2.1.2.3 Input Capacitor Selection
The input capacitors provide the AC current needed by the nearby power switch so that current provided by the upstream power supply does not carry a lot of AC content, generating less EMI. To the buck regulator in question, the input capacitor also prevents the drain voltage of the FET switch from dipping when the FET is turned on, therefore providing a healthy line rail for the LM26420 to work with. Because typically most of the AC current is provided by the local input capacitors, the power loss in those capacitors can be a concern. In the case of the LM26420 regulator, because the two channels operate 180° out of phase, the AC stress in the input capacitors is less than if they operated in phase. The measure for the AC stress is called input ripple RMS current. It is strongly recommended that at least one 10µF ceramic capacitor be placed next to each of the VIND pins. Bulk capacitors such as electrolytic capacitors or OSCON capacitors can be added to help stabilize the local line voltage, especially during large load transient events. As for the ceramic capacitors, use X7R or X5R types. They maintain most of their capacitance over a wide temperature range. Try to avoid sizes smaller than 0805. Otherwise significant drop in capacitance may be caused by the DC bias voltage. See Output Capacitor section for more information. The DC voltage rating of the ceramic capacitor should be higher than the highest input voltage.
Capacitor temperature is a major concern in board designs. While using a 10-µF or higher MLCC as the input capacitor is a good starting point, it is a good idea to check the temperature in the real thermal environment to make sure the capacitors are not overheated. Capacitor vendors may provide curves of ripple RMS current vs. temperature rise, based on a designated thermal impedance. In reality, the thermal impedance may be very different. So it is always a good idea to check the capacitor temperature on the board.
Because the duty cycles of the two channels may overlap, calculation of the input ripple RMS current is a little tedious — use Equation 14:
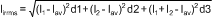
where
- I1 is Channel 1's maximum output current
- I2 is Channel 2's maximum output current
- d1 is the non-overlapping portion of Channel 1's duty cycle D1
- d2 is the non-overlapping portion of Channel 2's duty cycle D2
- d3 is the overlapping portion of the two duty cycles.
- Iav is the average input current
Iav= I1 × D1 + I2 × D2. To quickly determine the values of d1, d2 and d3, refer to the decision tree in Figure 37. To determine the duty cycle of each channel, use D = VOUT/VIN for a quick result or use the following equation for a more accurate result.
Example:
VIN = 5 V, VOUT1 = 3.3 V, IOUT1 = 2 A, VOUT2 = 1.2 V, IOUT2 = 1.5 A, RDS = 170 mΩ, RDC = 30 mΩ. (IOUT1 is the same as I1 in the input ripple RMS current equation, IOUT2 is the same as I2).
First, find out the duty cycles. Plug the numbers into the duty cycle equation and we get D1 = 0.75, and D2 = 0.33. Next, follow the decision tree in Figure 37 to find out the values of d1, d2 and d3. In this case, d1 = 0.5, d2 = D2 + 0.5 – D1 = 0.08, and d3 = D1 – 0.5 = 0.25. Iav = IOUT1 × D1 + IOUT2 × D2 = 1.995 A. Plug all the numbers into the input ripple RMS current equation and the result is IIR(rms) = 0.77 A.
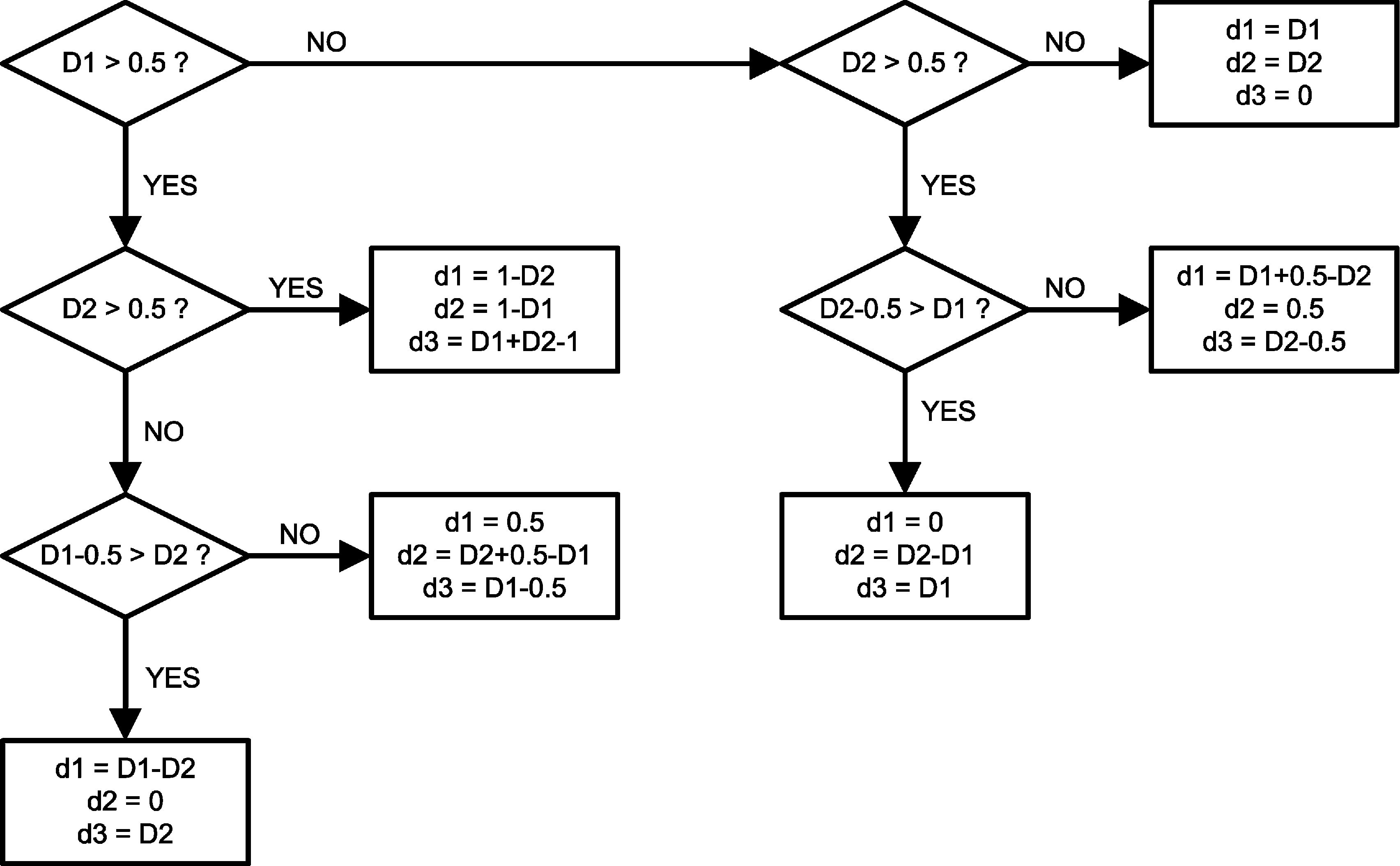 Figure 37. Determining D1, D2, And D3
Figure 37. Determining D1, D2, And D3