SLVAF30 February 2021 TPS55288 , TPS55288-Q1 , TPS552882 , TPS552882-Q1 , TPS61021A , TPS61022 , TPS61023 , TPS61088 , TPS61089 , TPS61178 , TPS61230A , TPS61235P , TPS61288 , TPS61378-Q1
3 Root Cause Analysis
The voltage spike shown in Figure 2-3 is caused by the ESR (effective series resistance) and ESL (effective series inductance) of the output capacitor. The Figure 3-1 shows the impedance of a 0805-package ceramic capacitor over frequency. Point A is the resonant frequency of the ESL and the capacitor.
The impedance of the capacitor is equal to its ESR which is approximately 3.5mΩ. The impedance of the capacitor increases linearly once the frequency is higher than 10 MHz. This is behavior of the ESL. From the impedance of point B and point C, the ESL is estimated to be 0.27nH.
 Figure 3-1 Characteristic of a Ceramic
Capacitor
Figure 3-1 Characteristic of a Ceramic
CapacitorThe voltage crossing the ESR is in proportion to the current through capacitor. A ceramic capacitor has only several milliohm resistances and normally there will be several ceramic capacitors in parallel. Thus, this voltage ripple caused by ESR is small and can be neglected.
The voltage crossing the ESL is in proportional to its di/dt, which could be very large. Because the switching frequency of a boost converter always tends to be as large as possible to reduce the solution size. The di/dt will also increase with the switching frequency to reduce the power loss in the IC.
Considering the ESL and the parasitic inductance of the PCB trace and IC package, the schematic of the boost converter power stage is shown in Figure 3-2 where LPAR1 is the sum of pin-out and PCB parasitic inductor and LPAR2 is the parasitic inductor of the GND pin;
 Figure 3-2 Boost Converter Power Stage With Parasitic Inductor
Figure 3-2 Boost Converter Power Stage With Parasitic InductorWhen Q1 turns off and SW node voltage is higher than VOUT, the inductor current starts to transit from Q1 to Q2. During the current transition period, the equivalent circuit is shown in Figure 3-3, where
- CQ1 represents parasitic capacitor of Q1. The turning-off time of Q1 is neglected.
- IL1 represents the inductor as inductor current is almost constant during the short transition period.
- VCOUT represent the voltage in the ideal capacitance portion of the output capacitor. the voltage is almost constant during this transition period.
 Figure 3-3 Simplified Model at Low Side MOSFET Turning Off
Figure 3-3 Simplified Model at Low Side MOSFET Turning OffThe Figure 3-3 can be further simplified to a LC circuit with initial inductor current IL1. The inductor value is the sum of all the parasitics inductor in the circuit. The capacitor is CQ1. So the voltage spike of the ESL is defined by Equation 2. The voltage spike is in proportinal to inductor current.
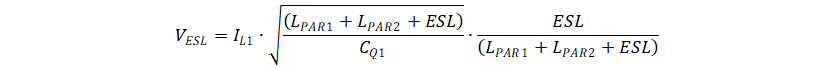
And the oscillation frequency is defined by Equation 3.
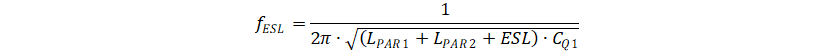
When Q1 turns on, the inductor current firstly transits from Q2 to Q1, then voltage Q1 quickly declines to zero. The simplified schematic during this period is shown in Figure 10, where CQ2 represents the parasitic capacitance of Q2 when it turns off.
 Figure 3-4 Simplified Model at Low Side MOSFET Turning On
Figure 3-4 Simplified Model at Low Side MOSFET Turning OnThe maximum voltage spike at ESL is defined by Equation 4. The circuit can also be simplified to a LC circuit. The VESL voltage level is in proportion to the boost output voltage, and the oscillation frequency is the same as Equation 3 because the CQ2 and CQ1 is similar.
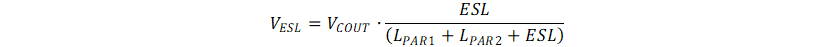
Taking TPS61022EVM as example, CQ1 and CQ2 are approximately 0.4 nF. LPAR1 is closed to 0.3 nH; LPAR2 is approximately 0.05 nH; ESL is approximately 0.09 nF as there are three capacitors in parallel. Thus, the LC oscillation frequency is up to 300 MHz.
At VIN=3.6V, VOUT=5V, IOUT=3A condition, the IL1 is about 4.4 A. The VESL spike at both Q1 turning on and turning off condition are approximately 0.75 V. however, the actual voltage spike from Figure 2-3 is lower than this calculation result, especially at Q1 turning-on condition. The main factor leading to the gap is the turning on/off time of the Q1. The turning on/off time of Q1 is at 5ns level. The greatly impacts the voltage spike caused by a 300-MHz LC ringing. It is hard to have an equation to calculate the voltage spike if considering the turning on/off time. A better method is simulation with PSPICE-FOR-TI or other tools.