SLUSBW3D March 2014 – December 2017 UCC28630 , UCC28631 , UCC28632 , UCC28633 , UCC28634
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Device Comparison Table
- 6 Pin Configuration and Functions
- 7 Specifications
-
8 Detailed Description
- 8.1 Overview
- 8.2 Functional Block Diagram
- 8.3
Feature Description
- 8.3.1 High-Voltage Current Source Start-Up Operation
- 8.3.2 AC Input UVLO / Brownout Protection
- 8.3.3 Active X-Capacitor Discharge (UCC28630 and UCC28633 only)
- 8.3.4 Magnetic Input and Output Voltage Sensing
- 8.3.5 Fixed-Point Magnetic Sense Sampling Error Sources
- 8.3.6 Magnetic Sense Resistor Network Calculations
- 8.3.7 Magnetic Sensing: Power Stage Design Constraints
- 8.3.8 Magnetic Sense Voltage Control Loop
- 8.3.9 Peak Current Mode Control
- 8.3.10 IPEAK Adjust vs. Line
- 8.3.11 Primary-Side Constant-Current Limit (CC Mode)
- 8.3.12 Primary-Side Overload Timer (UCC28630 only)
- 8.3.13 Overload Timer Adjustment (UCC28630 only)
- 8.3.14 CC-Mode IOUT(lim) Adjustment
- 8.3.15 Fault Protections
- 8.3.16 Pin-Fault Detection and Protection
- 8.3.17 Over-Temperature Protection
- 8.3.18 External Fault Input
- 8.3.19 External SD Pin Wake Input (except UCC28633)
- 8.3.20 External Wake Input at VSENSE Pin (UCC28633 Only)
- 8.3.21 Mode Control and Switching Frequency Modulation
- 8.3.22 Frequency Dither For EMI (except UCC28632)
- 8.4 Device Functional Modes
-
9 Applications and Implementation
- 9.1 Application Information
- 9.2
Typical Application
- 9.2.1 Notebook Adapter, 19.5 V, 65 W
- 9.2.2 UCC28630 Application Schematic
- 9.2.3 Design Requirements
- 9.2.4
Detailed Design Procedure
- 9.2.4.1 Custom Design With WEBENCH® Tools
- 9.2.4.2 Input Bulk Capacitance and Minimum Bulk Voltage
- 9.2.4.3 Transformer Turn Ratio
- 9.2.4.4 Transformer Magnetizing Inductance
- 9.2.4.5 Current Sense Resistor RCS
- 9.2.4.6 Transformer Constraint Verification
- 9.2.4.7 Transformer Selection and Design
- 9.2.4.8 Slope Compensation Verification
- 9.2.4.9 Power MOSFET and Output Rectifier Selection
- 9.2.4.10 Output Capacitor Selection
- 9.2.4.11 Calculation of CC Mode Limit Point
- 9.2.4.12 VDD Capacitor Selection
- 9.2.4.13 Magnetic Sense Resistor Network Selection
- 9.2.4.14 Output LED Pre-Load Resistor Calculation
- 9.2.5 External Wake Pulse Calculation at VSENSE Pin (UCC28633 Only)
- 9.2.6 Energy Star Average Efficiency and Standby Power
- 9.2.7 Application Performance Plots
- 9.3 Dos and Don'ts
- 10Power Supply Recommendations
- 11Layout
- 12Device and Documentation Support
- 13Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
- D|7
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9.2.4.7 Transformer Selection and Design
After determining the value of current sense resistor RCS, determine the maximum peak current at maximum demand point on the modulator. Accommodate for the IPEAK adjustment for frequency dithering. Use this value when calculating the margin for core saturation. In this case, IPK(sat) calculates to 4.13 A.
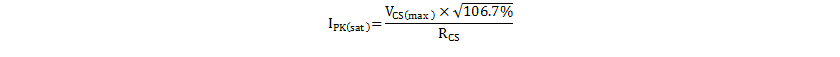
In subsequent calculations of required primary turns etc, the average maximum peak current, IPK(max) , during the frequency dither period should be used, which calculates to 4.0 A.
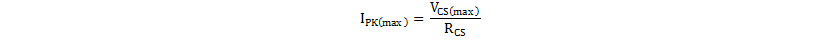
Knowing IPK(max), LPRI and the turns ratio, the choice of transformer size and core shape and type dictates the required number of primary, secondary and bias turns, and the size of the air-gap. Various trade-offs, design preferences, and transformer design targets (size, cost, target losses, etc.) influence the specific choice of transformer core in any given design.
In the case of the UCC28630EVM-572 (PWR572 EVM), core area-product geometry was used to choose the minimum core size available to meet the power level. The core geometry factor Kg is a figure-of-merit that reflects the core power capability, in terms of its physical size, shape and design. It combines the core effective cross-sectional area, Ae, winding window area, Aw, and the mean length per turn (MLT) of wire around the core.
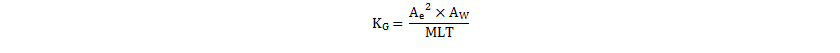
Estimate the required design core geometry, KG(des), using the required transformer inductance LPRI, maximum peak current IPK(max), allowed maximum core flux density Bmax and a target copper loss budget, PCU.
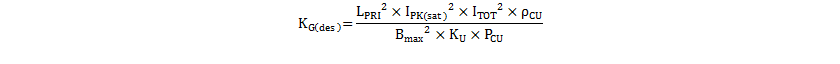
where
- ρcu is the resistivity of Copper (approximately 1.7 × 10-8 Ωm at room temperature, 2.2 × 10-8 Ωm at 100°C),
- Ku is a winding window utilization factor that accounts for the percentage of the window that is occupied by Copper
Ku can often be as low as 25%, due to the fill factor (gaps between wires), wire insulation (especially for triple-insulated wire), and the need for insulating tapes and EMC shielding layers. The estimate of the required core geometry needs an estimate of the aggregate total winding current ITOT. The analysis models the flyback transformer primary and secondary windings as a single lumped non-isolated inductor (such as a single winding buck inductor), only for the purpose of sizing the required core winding window to achieve the target copper loss. In this case, the secondary-side current amplitude reflects to the primary side so that aggregate total primary current. ITOT can be estimated in Equation 33.
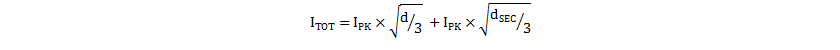
where
- d is the primary on-time duty cycle
- dSEC is the secondary-side flyback period duty cycle
At rated power and minimum bulk capacitor voltage, the inductance LPRI has been chosen to achieve boundary-mode conduction, therefore the duty cycle is given in Equation 34.
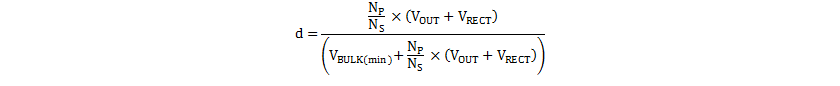
and
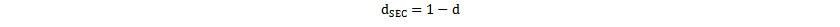
At the boundary conduction point, the primary peak current IPK is at the level set by the modulator, VCS(bcm). So from Equation 33, ITOT becomes Equation 36.
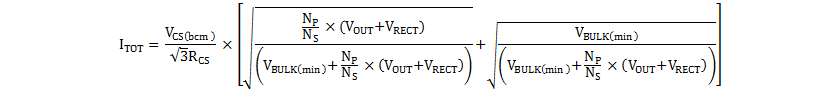
Equation 36 calculates ITOT as 2.6 A. Thus the required design KG(des), assuming KU of 25%, Bmax of 315 mT and a target of 1-W copper loss, is shown in Equation 37.
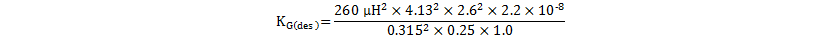
Equation 37 indicates that this design requires a core size and shape with a KG of more than 6.9 × 10-12. A review of commonly used cores indicated that the RM10/I core set meets this requirement. With Ae of 96.6 mm2, Aw of 44.2 mm2 and mean length per turn (MLT) of 52 mm, KG(RM10) is 7.9 × 10–12, giving some margin over the design target.
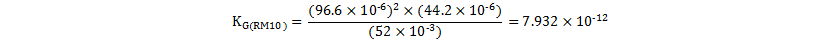
With the chosen core, the actual primary, secondary-side and bias turns can be calculated. The required primary turns depend on the allowed Bmax. For most power ferrites, a value in the region of 315 mT is commonly used.
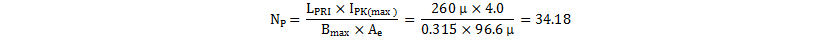
Round NP to 34. Now the required secondary-side turns can be calculated, using the previously calculated turns ratio per Equation 23.
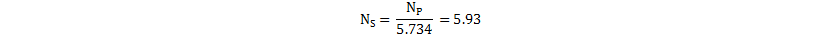
Again, NS is rounded to 6. Due to the integer rounding of the turns count, ensure that the actual turns ratio is within 5% of original target (if outside this range, secondary-side rectifier or primary MOSFET stress may be too high).
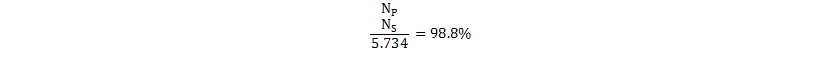
From Equation 24, the required bias turns can be calculated using Equation 42.
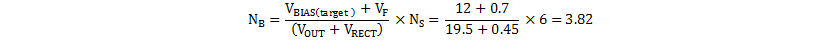
Again, NB is rounded to 4. The effect of integer scaling in the turns is verified by calculating the expected bias voltage versus target.
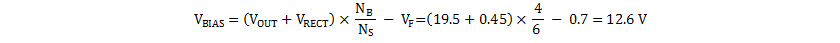
The VBIAS target was 12 V, so this is acceptable.
The required core inductance factor, AL, to achieve the target inductance can be calculated as in Equation 44. The transformer manufacturer uses this factor to gap the core center leg.
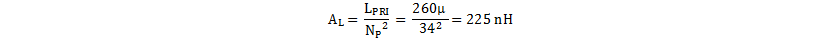
Finally, calculate the required air-gap length lg, based on the required inductance and the core geometry.
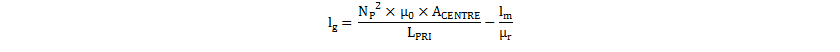
where
- μ0 is the permittivity of free-air
- μr is the relative permeability of the chosen core ferrite material
- ACENTRE is the cross-sectional area of the core center leg
- lm is the core average magnetic path length
For the RM10/I core in 3C95 material (chosen for low core loss over a wide temperature range), the required air-gap length is calaulated using Equation 46.
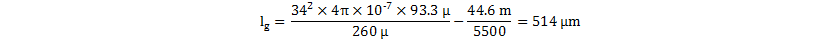
Typically, the air-gap calculation in Equation 45 underestimates lg, due to flux fringing in the air-gap. The fringing causes the affective area of the air-gap Ag to be somewhat larger than the ferrite core center leg ACENTRE, depending on the gap length. This difference requires an increase in the required air-gap length to get the required inductance, which results in a further increase in fringing. However use Equation 45 to determine an initial value for lg, which can then be used to estimate Ag. For round centre legs, the increase in effective area within the gap can be estimated empirically from Equation 47
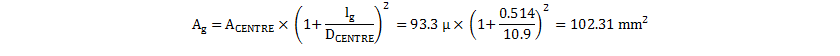
where
- DCENTRE is the center leg diameter
(For more information about this subject, download the paper Inductor and Flyback Transformer Design, Lloyd Dixon, TI Power Supply Design Seminar SLUP127).
Because Equation 45 assumes that Ag equals ACENTRE, it must be modified using Equation 48.
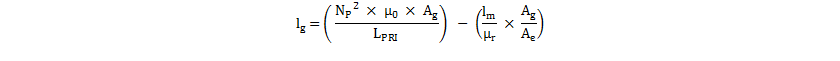
Re-iterating the air-gap calculation in Equation 49 .
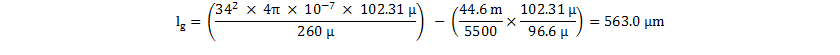
Typically, after the second iteration above in Equation 48, the estimated air-gap is very close to the required value. Further iterations can be made, but should not be necessary.