TIDUEU6B September   2020  – December 2021 OPA810

 

  1.   Description
  2.   Resources
  3.   Features
  4.   Applications
  5.   5
  6. 1System Description
    1. 1.1 Key System Specifications
  7. 2System Overview
    1. 2.1 Block Diagram
    2. 2.2 Highlighted Products
      1. 2.2.1 OPA2810
      2. 2.2.2 BUF634A
    3. 2.3 Design Considerations
      1. 2.3.1 Existing architecture
        1. 2.3.1.1 Circuit Stability Issue
        2. 2.3.1.2 Solution in Existing Architecture (Compensation Cap)
      2. 2.3.2 Proposed Design
        1. 2.3.2.1 Stability Analysis of the Proposed Design
          1. 2.3.2.1.1 Without Measurement of Voltage at Inverting Node of A2
          2. 2.3.2.1.2 With Measuring Voltage at Inverting Node of A2
        2. 2.3.2.2 RG = RF Settings and Respective Impedance Ranges
        3. 2.3.2.3 Impedance Measurement Procedure
          1. 2.3.2.3.1 Short Cal
          2. 2.3.2.3.2 Impedance Cal
          3. 2.3.2.3.3 100k Setting Calibration
          4. 2.3.2.3.4 Open Cal
          5. 2.3.2.3.5 Calculations
          6. 2.3.2.3.6 Correction in ZX
          7. 2.3.2.3.7 Data Acquisition and Processing
          8. 2.3.2.3.8 Mathematical Explanation
  8. 3Hardware, Software, Testing Requirements, and Test Results
    1. 3.1 Required Hardware and Software
      1. 3.1.1 Hardware
    2. 3.2 Testing and Results
      1. 3.2.1 Test Setup
      2. 3.2.2 Test Results
  9. 4Design Files
    1. 4.1 Schematics
    2. 4.2 Bill of Materials
    3. 4.3 PCB Layout Recommendations
      1. 4.3.1 Layout Prints
    4. 4.4 Altium Project
    5. 4.5 Gerber Files
    6. 4.6 Assembly Drawings
  10. 5Software Files
  11. 6Related Documentation
    1. 6.1 Trademarks
    2. 6.2 Third-Party Products Disclaimer
  12. 7Revision History

2.3.2.1 Stability Analysis of the Proposed Design

When the unknown impedance to be measured is capacitive i.e. CX, it forms the circuit shown in Figure 2-3. The transfer function of VF is given in Equation 4.

Equation 4. GUID-EC51B508-5B6C-47FF-A037-13DBA92ECEB8-low.gif
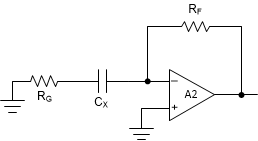GUID-3DF10C22-00BB-422F-8D2F-4985DE10BC82-low.gifFigure 2-7 Capacitive Measurement with Series Resistance

In comparison with Equation 2, Equation 4 shows that due to presence of RG, there is a pole-zero combination in the feedback path. The zero and pole frequencies in 1/β are given by,

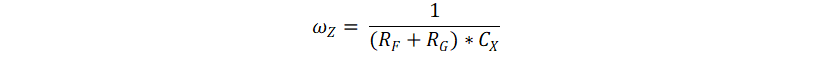
Equation 5. GUID-57D68358-7E28-4D19-B1D3-C46780CD9EDD-low.gif
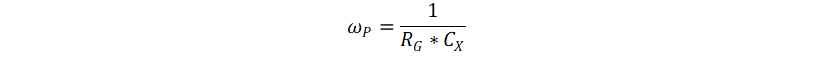
Equation 6. GUID-C73BD6D7-C8EF-4164-939F-6692953CC025-low.gif

The pole and zero frequencies hold the relation ωP = 2*ωZ because RG is equal to RF in every RG - RF setting.

GUID-20200717-CA0I-8SKQ-QFLH-R6HNVJ7H40M3-low.gifFigure 2-8 Bode Plot of Capacitive Measurement with Series Resistance

This provides the advantage of an inherent pole to cancel the zero. Figure 2-8 shows that the rate of closure of Aolβ is 20 dB/dec for almost all the CX. The exception for this fact is when fCL lies between fZ and fP. The RG - RF settings are selected such that this situation is avoided. This allows for a key factor of this design where ωP = 2*ωZ is independent of the value of CX. The measurement can be done in two ways as explained below,