When the spurs from the amplifier and filter are known, each individual spur can be directly added to the same spur from the ADC, as shown in Equation 14, to estimate the combined spur (spur amplitudes in dBc):

Equation 14.

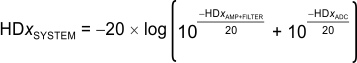
This calculation assumes the spurs are in phase, but usually provides a good estimate of the final combined distortion.

For example, if the spur of the amplifier and filter equals the spur of the ADC, then the combined spur is 6 dB higher. To minimize the amplifier contribution (< 1 dB) to the overall system distortion, the spur from the amplifier and filter must be approximately 19 dB lower in amplitude than that of the converter. The combined spur calculated in this manner is usually accurate to within ±6 dB of the actual implementation; however, higher variations can be detected as a result of phase shift in the filter, especially in second-order harmonic performance.

This worst-case spur calculation assumes that the amplifier and filter spur of interest is in phase with the corresponding spur in the ADC, such that the two spur amplitudes can be added linearly. There are two phase-shift mechanisms that cause the measured distortion performance of the amplifier-ADC chain to deviate from the expected performance calculated using Equation 14: common-mode phase shift and differential phase shift.

Common-mode phase shift is the phase shift detected equally in both branches of the differential signal path including the filter. Common-mode phase shift nullifies the basic assumption that the amplifier, filter, and ADC spur sources are in phase. This phase shift can lead to better performance than predicted when the spurs become phase shifted, and there is the potential for cancellation when the phase shift reaches 180°. However, a significant challenge exists in designing an amplifier-ADC interface circuit to take advantage of a common-mode phase shift for cancellation: the phase characteristic of the ADC spur sources are unknown, thus the necessary phase shift in the filter and signal path for cancellation is also unknown.

Differential phase shift is the difference in the phase response between the two branches of the differential filter signal path. Differential phase shift in the filter as a result of mismatched components caused by nominal tolerance can severely degrade the even-order distortion of the amplifier-ADC chain. This effect has the same result as mismatched path lengths for the two differential traces, and causes more phase shift in one path than the other. Ideally, the phase response over frequency through the two sides of a differential signal path are identical, such that even-order harmonics remain optimally out of phase and cancel when the signal is taken differentially. However, if one side has more phase shift than the other, then the even-order harmonic cancellation is not as effective.

Single-order RC filters cause very little differential phase shift with nominal tolerances of 5% or less, but higher-order LC filters are very sensitive to component mismatch. For instance, a third-order Butterworth band-pass filter with a 100-MHz center frequency and a 20-MHz bandwidth creates as much as 20° of differential phase imbalance in a SPICE Monte Carlo analysis with 2% component tolerances. Therefore, although a prototype may work, production variance is unacceptable. In ac-coupled applications that require second- and higher-order filters between the LMH5401 and the ADC, a transformer or balun is recommended at the ADC input to restore the phase balance. For DC-coupled applications where a transformer or balun at the ADC input cannot be used, using first- or second-order filters is recommended to minimize the effect of differential phase shift because of the component tolerance.