CRC can be used on transmission of long data lengths into the hundreds, thousands or even longer number of bits. The generic CRC code being discussed for embedded applications is based on a short data transmission length of 32-bits or less in most cases. The data are byte oriented with transmission in byte multiples for a maximum of 4 bytes in the case of a 32-bit transfer. If the maximum data transfer length is a multiple of 8-bits, the CRC computations can be accomplished using pointers to a memory array.

As the CRC is a division of the polynomial into the data, the initial part of the discussion describes the process of determining the remainder using long division. The data value transmitted is divided by the polynomial in use. When the data is the dividend the initial value used is zero in this case. This would be the same as 0h exclusive-OR (XOR) with the data and the result being equal to the data. The remainder from the completed long division where the divisor is the polynomial and the dividend is the data becomes the computed CRC value. So the data (dividend) is divided by the polynomial (divisor) and the computed result is the quotient. The remainder from the computation is the CRC value.

When the initial value is zero and the data has leading zeros, the CRC computation would ignore the leading zeros in the computation. To make the computation of CRC more robust to include any leading zeros, an initial value other than zero is used. The most common non-zero initial value is all 1's for the size of the CRC being used. The non-zero initial value for 8-bit CRC is FFh, and FFFFh for 16-bit CRC. The initial value for the computation is specified in the ADC device datasheet. The initial value and the data are then XOR'ed together to create the dividend.

The implemented polynomial for ADCs is often a standard CRC polynomial, such as CRC-8-ATM or CRC-16-CCITT. These polynomials have been shown to be effective for data transmission integrity checks. Often one of these standard CRC algorithms are implemented in embedded microcontrollers for faster computation. The ADS122C04 uses the 16-bit polynomial CRC-16-CCITT which has been commonly used in communication data transfers. The polynomial is x¹⁶ + x¹² + x⁵ + 1 and is equivalent to 10001000000100001b. The generated CRC result is the remainder of the long division of the data divided by the polynomial. This discussion will not go into detail on the process of modulo 2 math other than to say a subtraction of two values becomes an XOR operation.

The initial 16-bit starting value for the ADS122C04 is given in the datasheet as FFFFh. The example in Figure 3-1 uses a data value that is 24-bits in length similar to a conversion result. The example uses a value of 4E6878h for the data.

As the final result will be a remainder of 16-bits, the initial value is appended with zeroes so that the total length will consist of the length of the data plus the 16-bit remainder.

1. Initial value = 0xFFFF (as per ADS122C04 datasheet)
2. Right pad the initial value with 24 "0"s so that the total length of the initial value is the length of the conversion data plus the length of the CRC (40 bits total)
3. XOR initial value left aligned with converted value: FFFF000000h XOR 4E68780000h = 0xB197780000 (See Figure 3-1)
4. Divide the result of step 2 by the polynomial: B197780000h ÷ 11021h and take the remainder B72Ch as the computed CRC value

The process of dividing the divisor into the dividend results in a remainder of B72Ch as shown in Figure 3-2 which would be the CRC value transmitted by the ADS122C04 following the transmission of the conversion data.

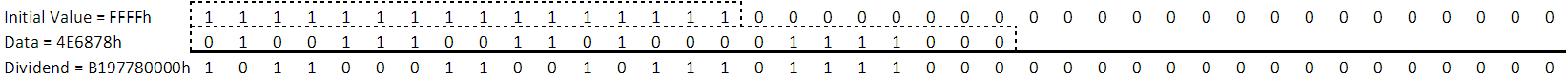Figure 3-1 Example of Computing the Starting Value for CRC Computation by XOR of the Initial Value and Data

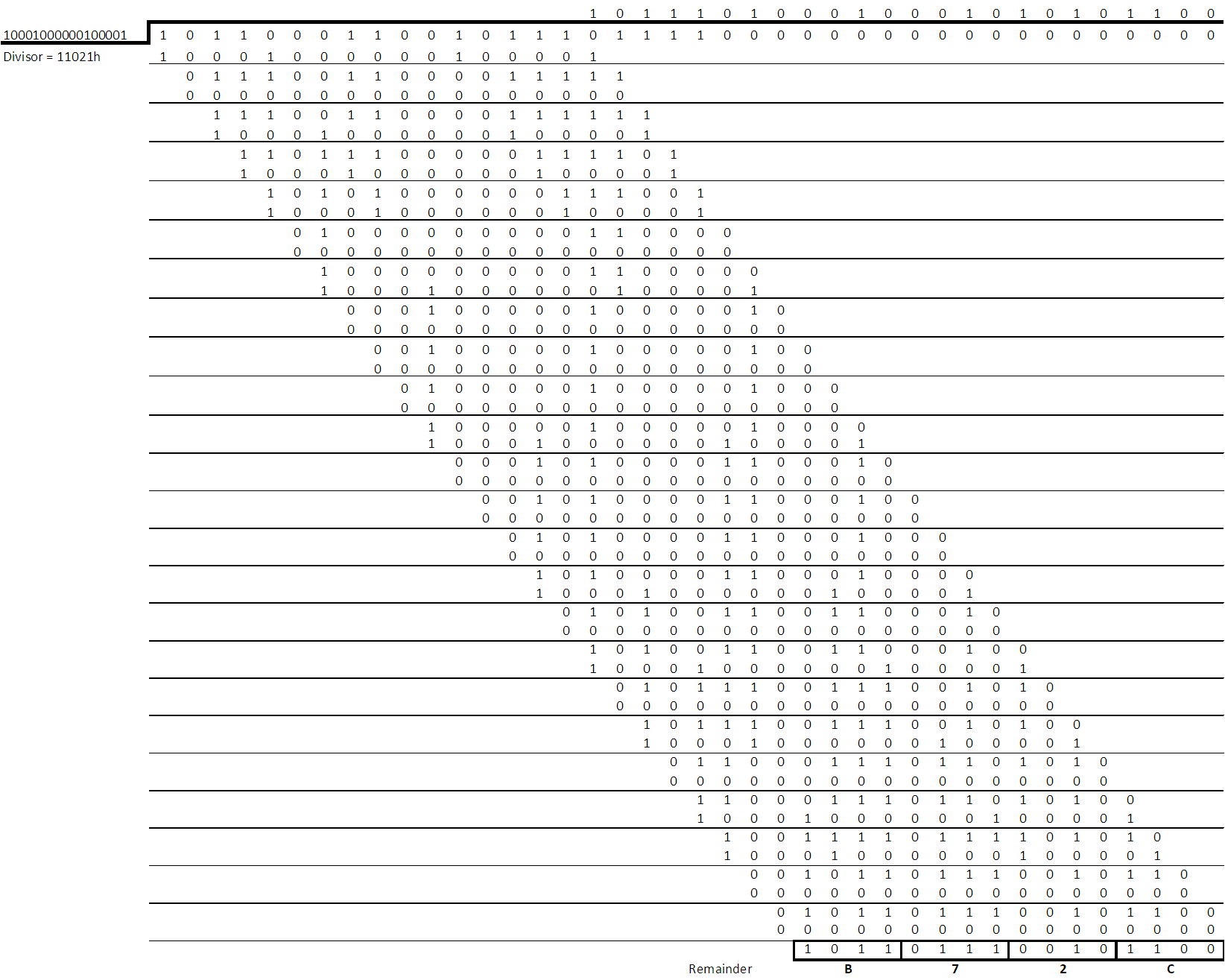Figure 3-2 Binary Long Division of Two Polynomials of Binary Coefficients

For ADC devices transmitting data serially, the hardware implementation is often through a shift register with the CRC computed as the data are shifted out. Depending on the type of interface, the data may need to be reversed or reflected for the CRC computation. Data reflection is simply the swapping of the order of the bits transmitted. Why the order is important is discussed in more detail when comparing the CRC computations of the ADS122C04 (I²C) and the ADS122U04 (UART) devices in Section 3.1.3. The difference in data transmission is the UART is LSB first and I²C is MSB first. What becomes complicated is the reading of the UART receive buffer when transferred to memory. When reading the receive buffer the order of bits are reversed, or reflected, from the order transmitted for each byte. When computing the CRC the proper order of the bits as transmitted must be used.

The microcontroller may also use a hardware implementation for computing CRC. Besides CRC hardware implementations, the embedded processor code can accomplish the same task as long division using a similar XOR process and rotating through each bit and byte returning the CRC as the remainder. The XOR process takes considerable time within the function as a bitwise process. Another common method is to use a lookup table for processing the values. Both the XOR bitwise and lookup table methods are discussed.