SBAA106A June 2020 – August 2021 ADS112C04 , ADS112U04 , ADS114S06 , ADS114S08 , ADS122C04 , ADS122U04 , ADS1235 , ADS1235-Q1 , ADS124S06 , ADS124S08 , ADS1259 , ADS1259-Q1 , ADS125H01 , ADS125H02 , ADS1260 , ADS1260-Q1 , ADS1261 , ADS1262 , ADS1263 , ADS127L01 , ADS131A02 , ADS131A04 , ADS131M04 , ADS131M06 , ADS131M08
3.1.1 Using XOR Bitwise Computation
Software bitwise functions ignore the most high order bit in the polynomial value. The bit can be ignored as the highest order bit is shifted out before the remainder is XORed. For demonstration, the polynomial for CRC-16-CCITT is x16 + x12 + x5 + 1 (11021h) and is represented by 10001000000100001b. However, the highest order bit is dropped and the value used for computation in the bitwise operation becomes 1021h.
 Figure 3-3 CRC-16-CCITT Hardware Implementation
Figure 3-3 CRC-16-CCITT Hardware ImplementationFor the 8-bit CRC-8-ATM (HEC) the polynomial is X8 + X2 + X + 1 (107h) and is represented by 100000111b. Again, the highest order bit is ignored and the value to use in the bitwise operation is 7h.
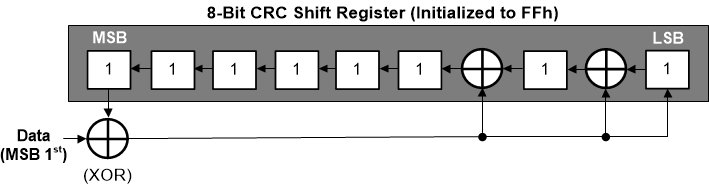 Figure 3-4 CRC-8-ATM (HEC) Hardware Implementation
Figure 3-4 CRC-8-ATM (HEC) Hardware ImplementationThe following code function is shown for CRC-16-CCITT, but can be easily adapted to other polynomials and lengths. The function replicates the hardware implementation and returns a value based on the size of the CRC length and is signified by the type definition for crc_t. For the code example the returned value is an unsigned 16-bit value. Parameters passed are the pointer to the data packet to be computed and the length of the data packet in number of bytes. The function processes each byte of data by an XOR of each bit with the remainder. The initial value of the REMAINDER_INIT is the starting seed value and will differ depending on what ADC is being used.
typedef uint16_t crc_t; // for 8 bits, use uint8_t
#define POLYNOMIAL 0x1021 // CRC16-CCITT, but for 8 bits use CRC-8-ATM(HEC),
// and the polynomial value 0x07
#define REMAINDER_INIT 0xFFFF // 0xFFFF for 16-bit CRC on ADS1xC04, ADS1x2U04
// 0xFF for 8 bit CRC on ADS1260, ADS1261, ADS1235
// 0x00 for 8 bit CRC on ADS124S0x, ADS114S0x, ADS1262, ADS1263
#define WIDTH (8 * sizeof(crc_t))
/**
* Computes CRC for an array of data bytes.
*
* \details CRC computation of a series of bytes using XOR with desired polynomial.
*
* \param uint8_t *data, pointer to data array.
* \param uint32_t length, of data array.
*
* \returns crc_t remainder.
*/
crc_t crcBitwise(uint8_t *data, uint32_t length)
{
crc_t remainder = REMAINDER_INIT;
uint32_t byte, bit;
// For each byte in data packet, perform long
// division of polynomials
for(byte = 0; byte < length; byte++)
{
remainder ^= (data[byte] << (WIDTH - 8)); // Get next byte into remainder
for(bit = 8; bit > 0; bit--) // For each bit in the remainder
{
if(remainder & (1 << (WIDTH - 1)))
remainder = (remainder << 1) ^ POLYNOMIAL; // If the top bit is set, left shift
// the remainder and XOR it with the
else // divisor and store the result in
// the remainder
remainder = (remainder << 1); // If the top bit is clear, left shift
// the remainder
}
}
return remainder;
} The code example is useful for determining the CRC remainder for the data. The computed remainder is required for devices that have both ingoing and outgoing CRC data integrity checks. However, if the data is only being validated for transmission from the ADC, such as conversion data, the CRC value transmitted can be added to the data array. If the CRC remainder is included in the computation and if the CRC matches both the computed and transmitted values, the remainder will be zero. In other words there is an important property of CRC computation where shifting in a matching byte forces the value in the CRC shift register to zero. A non-zero result would indicate an error in transmission. Using this method may simplify the validation by eliminating the direct comparison of the CRC from the transmission and the computed CRC.