SLVSDV8 July 2017 TPS54424
PRODUCTION DATA.
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Pin Configuration and Functions
- 6 Specifications
-
7 Detailed Description
- 7.1 Overview
- 7.2 Functional Block Diagram
- 7.3
Feature Description
- 7.3.1 Fixed Frequency PWM Control
- 7.3.2 Continuous Conduction Mode Operation (CCM)
- 7.3.3 VIN Pins and VIN UVLO
- 7.3.4 Voltage Reference and Adjusting the Output Voltage
- 7.3.5 Error Amplifier
- 7.3.6 Enable and Adjustable UVLO
- 7.3.7 Soft Start and Tracking
- 7.3.8 Safe Start-up into Pre-Biased Outputs
- 7.3.9 Power Good
- 7.3.10 Sequencing (SS/TRK)
- 7.3.11 Adjustable Switching Frequency (RT Mode)
- 7.3.12 Synchronization (CLK Mode)
- 7.3.13 Bootstrap Voltage and 100% Duty Cycle Operation (BOOT)
- 7.3.14 Output Overvoltage Protection (OVP)
- 7.3.15 Overcurrent Protection
- 7.4 Device Functional Modes
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Application
- 8.2.1 Design Requirements
- 8.2.2
Detailed Design Procedure
- 8.2.2.1 Custom Design With WEBENCH® Tools
- 8.2.2.2 Switching Frequency
- 8.2.2.3 Output Inductor Selection
- 8.2.2.4 Output Capacitor
- 8.2.2.5 Input Capacitor
- 8.2.2.6 Output Voltage Resistors Selection
- 8.2.2.7 Soft-start Capacitor Selection
- 8.2.2.8 Undervoltage Lockout Set Point
- 8.2.2.9 Bootstrap Capacitor Selection
- 8.2.2.10 PGOOD Pull-up Resistor
- 8.2.2.11 Compensation
- 8.2.3 Application Curves
- 9 Power Supply Recommendations
- 10Layout
- 11Device and Documentation Support
- 12Mechanical, Packaging, and Orderable Information
Package Options
Refer to the PDF data sheet for device specific package drawings
Mechanical Data (Package|Pins)
- RNV|18
Thermal pad, mechanical data (Package|Pins)
Orderable Information
8.2.2.11 Compensation
There are several methods used to compensate DC - DC regulators. The method presented here is easy to calculate and ignores the effects of the slope compensation internal to the device. Because the slope compensation is ignored, the actual cross-over frequency will usually be lower than the cross-over frequency used in the calculations. This method assumes the cross-over frequency is between the modulator pole and the ESR zero and the ESR zero is at least 10 times greater the modulator pole. This is the case when using low ESR output capacitors. Use the WEBENCH® software for more accurate loop compensation. These tools include a more comprehensive model of the control loop.
To get started, the modulator pole, fpmod, and the ESR zero, fz1 must be calculated using Equation 26 and Equation 27. For Cout, use a derated value of 80 μF and an ESR of 2 mΩ. Use equations Equation 28 and Equation 29, to estimate a starting point for the crossover frequency, fco, to design the compensation. For the example design, fpmod is 4.4 kHz and fzmod is 995 kHz. Equation 28 is the geometric mean of the modulator pole and the ESR zero. Equation 29 is the mean of modulator pole and one half the switching frequency. Equation 28 yields 66 kHz and Equation 29 gives 39 kHz. Use the lower value of Equation 28 or Equation 29 for an initial crossover frequency. Next, the compensation components are calculated. A resistor in series with a capacitor is used to create a compensating zero. A capacitor in parallel to these two components forms the compensating pole.
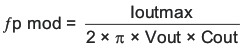
vertical spacer
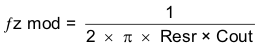
vertical spacer

vertical spacer

To determine the compensation resistor, R5, use Equation 30. R5 is calculated to be 3.17 kΩ and the closest standard value 3.16 kΩ. Use Equation 31 to set the compensation zero to the modulator pole frequency. Equation 31 yields 11.4 nF for compensating capacitor C18 and the closest standard value is 0.012 µF.
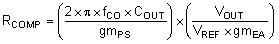
Where:
- Power stage transconductance, gmPS = 17 A/V
- VOUT = 1.8 V
- VREF = 0.6 V
- Error amplifier transconductance, gmEA = 1100 µA/V
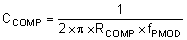
A compensation pole is implemented using an additional capacitor C17 in parallel with the series combination of R5 and C18. This capacitor is recommended to help filter any noise that may couple to the COMP voltage signal. Use the larger value of Equation 32 and Equation 33 to calculate the C17 and to set the compensation pole. C17 is calculated to be the largest of 41 pF and 134 pF. The closest standard value is 120 pF.
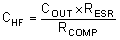
vertical spacer
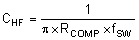
Type III compensation can be used by adding the feed forward capacitor C19 in parallel with the upper feedback resistor. Type III compensation adds phase boost above what is possible from type II compensation because it places an additional zero/pole pair. The zero/pole pair is not independent. As a result once the zero location is chosen, the pole is fixed as well. The zero is placed at 1/2 the fSW by calculating the value of C19 with Equation 34. The calculated value is 37 pF and the closest standard value is 39 pF. It is possible to use larger feedforward capacitors to further improve the transient response but care should be taken to ensure there is a minimum of -10 dB gain margin at 1/2 the fSW in all operating conditions. The feedforward capacitor injects noise on the output into the FB pin and this added noise can result in more jitter at the switching node. To little gain margin can cause a repeated wide and narrow pulse behavior. This example design does not use the optional feedforward capacitor.
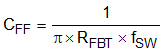
The initial compensation based on these calculations is R5 = 3.16 kΩ, C18 = 0.012 µF, and C17 = 120 pF. These values yield a stable design but after testing the real circuit these values were changed to target a higher crossover frequency to improve transient response performance. The crossover frequency is increased by increasing the value of R5 and decreasing the value of the compensation capacitors. The final values used in this example are R5 = 3.48 kΩ, C18 = 8200 pF, and C17 = 68 pF.