JAJSJT8C May 2020 – June 2021 TPS543620
PRODUCTION DATA
- 1 特長
- 2 アプリケーション
- 3 概要
- 4 Revision History
- 5 Pin Configuration and Functions
- 6 Specifications
-
7 Detailed Description
- 7.1 Overview
- 7.2 Functional Block Diagram
- 7.3
Feature Description
- 7.3.1 VIN Pins and VIN UVLO
- 7.3.2 Enable and Adjustable UVLO
- 7.3.3 Adjusting the Output Voltage
- 7.3.4 Switching Frequency Selection
- 7.3.5 Switching Frequency Synchronization to an External Clock
- 7.3.6 Ramp Amplitude Selection
- 7.3.7 Soft Start and Prebiased Output Start-up
- 7.3.8 Mode Pin
- 7.3.9 Power Good (PGOOD)
- 7.3.10 Current Protection
- 7.3.11 Output Overvoltage and Undervoltage Protection
- 7.3.12 Overtemperature Protection
- 7.3.13 Output Voltage Discharge
- 7.3.14 Low-Side MOSFET Resistance Scaling
- 7.4 Device Functional Modes
-
8 Application and Implementation
- 8.1 Application Information
- 8.2
Typical Applications
- 8.2.1
1.0-V Output, 1-MHz Application
- 8.2.1.1 Design Requirements
- 8.2.1.2
Detailed Design Procedure
- 8.2.1.2.1 Switching Frequency
- 8.2.1.2.2 Output Inductor Selection
- 8.2.1.2.3 Output Capacitor
- 8.2.1.2.4 Input Capacitor
- 8.2.1.2.5 Adjustable Undervoltage Lockout
- 8.2.1.2.6 Output Voltage Resistors Selection
- 8.2.1.2.7 Bootstrap Capacitor Selection
- 8.2.1.2.8 BP5 Capacitor Selection
- 8.2.1.2.9 PGOOD Pullup Resistor
- 8.2.1.2.10 Current Limit Selection
- 8.2.1.2.11 Soft-Start Time Selection
- 8.2.1.2.12 Ramp Selection and Control Loop Stability
- 8.2.1.2.13 MODE Pin
- 8.2.1.3 Application Curves
- 8.2.2 1.0-V Output, 1.5-MHz Application
- 8.2.3 3.3-V Output, 1.0-MHz Application
- 8.2.4 1.8-V Output, 1.0-MHz Typical Application
- 8.2.5 5.0-V Output, 1.0-MHz Typical Application
- 8.2.1
1.0-V Output, 1-MHz Application
- 9 Power Supply Recommendations
- 10Layout
- 11Device and Documentation Support
- 12Mechanical, Packaging, and Orderable Information
8.2.1.2.3 Output Capacitor
There are two primary considerations for selecting the value of the output capacitor: the output voltage ripple and how the regulator responds to a large change in load current. The output capacitance needs to be selected based on the more stringent of these criteria.
The desired response to a large change in the load current is the first criteria and is typically the most stringent. A regulator does not respond immediately to a large, fast increase or decrease in load current. The output capacitor supplies or absorbs charge until the regulator responds to the load step. The control loop needs to sense the change in the output voltage then adjust the peak switch current in response to the change in load. The minimum output capacitance is selected based on an estimate of the loop bandwidth. Typically the loop bandwidth is near fSW / 10. Equation 10 estimates the minimum output capacitance necessary, where ΔIOUT is the change in output current and ΔVOUT is the allowable change in the output voltage.
For this example, the transient load response is specified as a 3% change in VOUT for a load step of 3 A. Therefore, ΔIOUT is 3 A and ΔVOUT is 30 mV. Using this target gives a minimum capacitance of 159 μF. This value does not take the ESR of the output capacitor into account in the output voltage change. For ceramic capacitors, the effect of the ESR can be small enough to be ignored. Aluminum electrolytic and tantalum capacitors have higher ESR that must be considered for load step response.
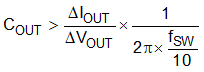
In addition to the loop bandwidth, it is possible for the inductor current slew rate to limit how quickly the regulator responds to the load step. For low duty cycle applications, the time it takes for the inductor current to ramp down after a load step down can be the limiting factor. Equation 11 estimates the minimum output capacitance necessary to limit the change in the output voltage after a load step down. Using the 0.6-µH inductance selected gives a minimum capacitance of 90 µF.
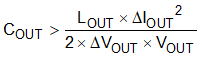
Equation 12 calculates the minimum output capacitance needed to meet the output voltage ripple specification. In this case, the target maximum steady state output voltage ripple is 10 mV. Under this requirement, Equation 12 yields 19 µF.
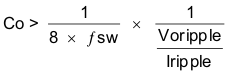
where
- ΔIOUT is the change in output current
- ΔVOUT is the allowable change in the output voltage
- fsw is the regulators switching frequency
- Voripple is the maximum allowable steady state output voltage ripple
- Iripple is the inductor ripple current
Lastly, if an application does not have a strict load transient response or output ripple requirement, a minimum amount of capacitance is still required to ensure the control loop is stable with the lowest gain ramp setting on the MODE pin. Equation 13 estimates the minimum capacitance needed for loop stability. This equation sets the minimum amount of capacitance by keeping the LC frequency relative to the switching frequency at a minimum value. See Figure 8-3 for the limit versus output voltage with the lowest gain ramp setting of 1 pF. With a 1-V output, the minimum ratio is 35 and with this ratio, Equation 13 gives a minimum capacitance of 52 µF.
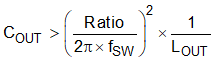
Equation 14 calculates the maximum combined ESR the output capacitors can have to meet the output voltage ripple specification and this shows the ESR should be less than 6 mΩ. In this case, ceramic capacitors are used and the combined ESR of the ceramic capacitors in parallel is much less than is needed to meet the ripple. Capacitors also have limits to the amount of ripple current they can handle without producing excess heat and failing. An output capacitor that can support the inductor ripple current must be specified. The capacitor data sheet specifies the RMS value of the maximum ripple current. Equation 15 can be used to calculate the RMS ripple current the output capacitor needs to support. For this application, Equation 15 yields 445 mA and ceramic capacitors typically have a ripple current rating much higher than this.
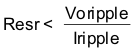
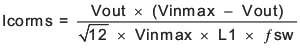
Select X5R and X7R ceramic dielectrics or equivalent for power regulator capacitors since they have a high capacitance-to-volume ratio and are fairly stable over temperature. The output capacitor must also be selected with the DC bias and AC voltage derating taken into account. The derated capacitance value of a ceramic capacitor due to DC voltage bias and AC RMS voltage is usually found on the capacitor manufacturer's website. For this application example, two 22-µF, 10-V, X7S, 0805 and two 47-µF, 6.3-V, X7R, 1210 ceramic capacitors each with 2 mΩ of ESR are used. The two 22-µF capacitors are used since they have a higher resonance frequency and can help reduce the output ripple caused by parasitic inductance. With the four parallel capacitors, the estimated effective output capacitance after derating using the capacitor manufacturer's website is 142 µF. There is almost no DC bias derating at 1 V. This design was able to use less than the calculated minimum because the loop crossover frequency was above the fSW / 10 estimate as shown in the Load Transient graph in the Application Curves.