SBOA345 June 2021 ADC10D1000QML-SP , ADC12D1600QML-SP , ADC12D1620QML-SP , INA1620 , OPA132 , OPA134 , OPA1602 , OPA1604 , OPA1611 , OPA1612 , OPA1622 , OPA1632 , OPA1637 , OPA1641 , OPA1642 , OPA1644 , OPA1652 , OPA1654 , OPA1655 , OPA1656 , OPA1662 , OPA1664 , OPA1671 , OPA1677 , OPA1678 , OPA1679 , OPA1688 , OPA1692 , OPA2132 , OPA2134 , OPA4132 , OPA4134
1 Thermal Noise
Resistors can be a major contribution to the overall noise of an audio circuit. The noise generated from a resistor, also known as thermal noise, is noise generated by the random motion of charges within the resistor. We can calculate the noise generated by an ideal resistor using Equation 1.
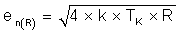
Where
- en(R) = Noise spectral density from resistance in nV/√Hz
- k = Boltzmann’s constant 1.38 x 10-23 J/K
- Tk = Temperature in Kelvin
- R = The input resistance referred to the non-inverting terminal of the amplifier
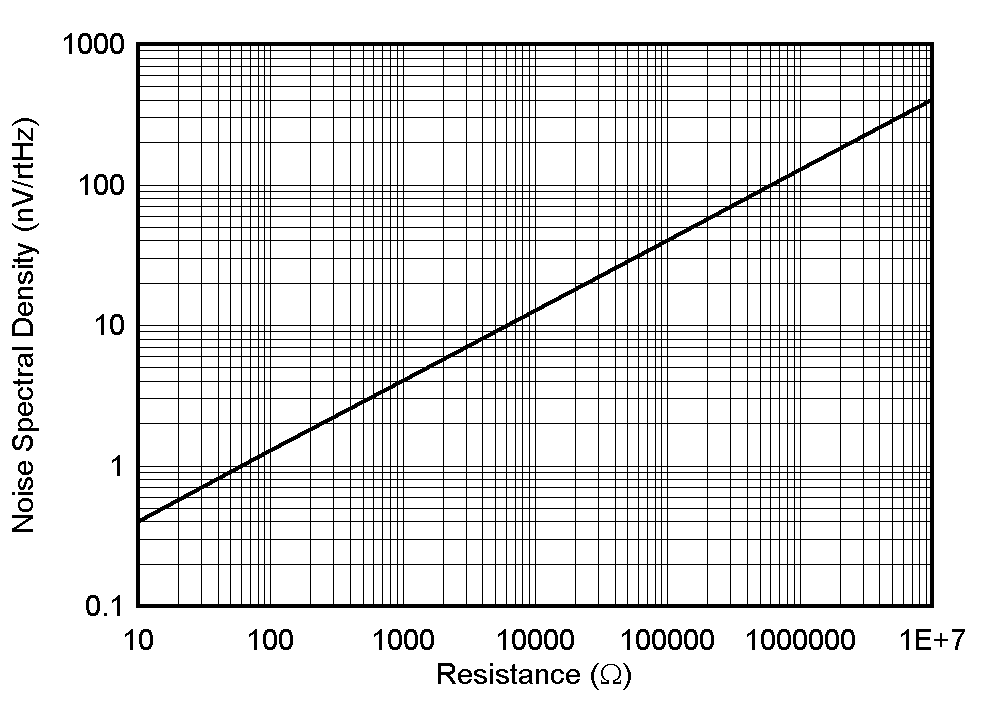Figure 1-1 Voltage Noise Density CurveFigure 1-1 displays the relationship between noise spectral density (in nV/√Hz) and resistance (in ohms) plotted for T = 25°C (298K) with varying source resistance values. At just 1k ohms of source resistance the voltage noise is already at 4nV/√Hz.
It’s important to note that an ideal resistor will exhibit predictable noise density that is flat across the frequency spectrum. Multiplying Equation 1 by the noise bandwidth yields RMS. The noise bandwidth is the bandwidth of your circuit. This bandwidth can either be set by the operational amplifier internal circuitry or by using a filter. This RMS noise calculation is shown in Equation 2.
