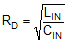SNVSB29C October 2018 – June 2021 LM5143-Q1
PRODUCTION DATA
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Description (continued)
- 6 Pin Configuration and Functions
- 7 Specifications
-
8 Detailed Description
- 8.1 Overview
- 8.2 Functional Block Diagram
- 8.3
Feature Description
- 8.3.1 Input Voltage Range (VIN)
- 8.3.2 High-Voltage Bias Supply Regulator (VCC, VCCX, VDDA)
- 8.3.3 Enable (EN1, EN2)
- 8.3.4 Power Good Monitor (PG1, PG2)
- 8.3.5 Switching Frequency (RT)
- 8.3.6 Clock Synchronization (DEMB)
- 8.3.7 Synchronization Out (SYNCOUT)
- 8.3.8 Spread Spectrum Frequency Modulation (DITH)
- 8.3.9 Configurable Soft Start (SS1, SS2)
- 8.3.10 Output Voltage Setpoint (FB1, FB2)
- 8.3.11 Minimum Controllable On-Time
- 8.3.12 Error Amplifier and PWM Comparator (FB1, FB2, COMP1, COMP2)
- 8.3.13 Slope Compensation
- 8.3.14 Inductor Current Sense (CS1, VOUT1, CS2, VOUT2)
- 8.3.15 Hiccup Mode Current Limiting (RES)
- 8.3.16 High-Side and Low-Side Gate Drivers (HO1/2, LO1/2, HOL1/2, LOL1/2)
- 8.3.17 Output Configurations (MODE, FB2)
- 8.4 Device Functional Modes
-
9 Application and Implementation
- 9.1 Application Information
- 9.2 Typical Applications
- 10Power Supply Recommendations
- 11Layout
- 12Device and Documentation Support
- 13Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
- RWG|40
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9.1.1.5 EMI Filter
Switching regulators exhibit negative input impedance, which is lowest at the minimum input voltage. An underdamped LC filter exhibits a high output impedance at the resonant frequency of the filter. For stability, the filter output impedance must be less than the absolute value of the converter input impedance.
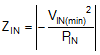
The EMI filter design steps are as follows:
- Calculate the required attenuation of the EMI filter at the switching frequency, where CIN represents the existing capacitance at the input of the switching converter.
- The input filter inductor LIN is usually selected between 1 μH and 10 μH, but it can be lower to reduce losses in a high-current design.
- Calculate input filter capacitor CF.
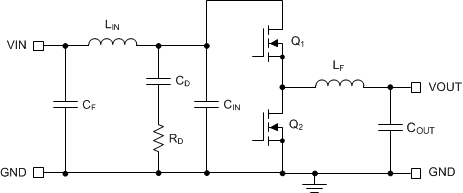 Figure 9-2 Buck Regulator With π-Stage EMI Filter
Figure 9-2 Buck Regulator With π-Stage EMI FilterBy calculating the first harmonic current from the Fourier series of the input current waveform and multiplying it by the input impedance (the impedance is defined by the existing input capacitor CIN), a formula is derived to obtain the required attenuation as shown by Equation 23.
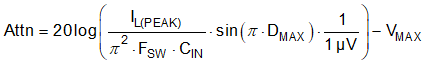
where
- VMAX is the allowed dBμV noise level for the applicable conducted EMI specification (for example, CISPR 25 Class 5)
- CIN is the existing input capacitance of the buck regulator
- DMAX is the maximum duty cycle
- IPEAK is the peak inductor current
For filter design purposes, the current at the input can be modeled as a square-wave. Determine the EMI filter capacitance CF from Equation 24.
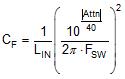
Adding an input filter to a switching regulator modifies the control-to-output transfer function. The output impedance of the filter must be sufficiently small such that the input filter does not significantly affect the loop gain of the buck converter. The impedance peaks at the filter resonant frequency. Use Equation 25 to calculate the resonant frequency of the filter.
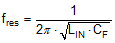
The purpose of RD is to reduce the peak output impedance of the filter at its resonant frequency. Capacitor CD blocks the DC component of the input voltage to avoid excessive power dissipation in RD. Capacitor CD must have lower impedance than RD at the resonant frequency with a capacitance value greater than that of the input capacitor CIN. This prevents CIN from interfering with the cutoff frequency of the main filter. Added damping is needed when the output impedance of the filter is high at the resonant frequency (Q of the filter formed by LIN and CIN is too high). An electrolytic capacitor CD can be used for damping with a value given by Equation 26.
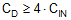
Use Equation 27 to select the damping resistor RD.