SLUSA12G December 2009 – November 2022 UCC28C40-Q1 , UCC28C41-Q1 , UCC28C42-Q1 , UCC28C43-Q1 , UCC28C44-Q1 , UCC28C45-Q1
PRODUCTION DATA
- 1 Features
- 2 Applications
- 3 Description
- 4 Revision History
- 5 Device Comparison Table
- 6 Pin Configuration and Functions
- 7 Specifications
-
8 Detailed Description
- 8.1 Overview
- 8.2 Functional Block Diagram
- 8.3 Feature Description
- 8.4 Device Functional Modes
-
9 Application and Implementation
- 9.1 Application Information
- 9.2
Typical Application
- 9.2.1 Design Requirements
- 9.2.2
Detailed Design Procedure
- 9.2.2.1 Custom Design With WEBENCH® Tools
- 9.2.2.2 Input Bulk Capacitor and Minimum Bulk Voltage
- 9.2.2.3 Transformer Turns Ratio and Maximum Duty CycleG
- 9.2.2.4 Transformer Inductance and Peak Currents
- 9.2.2.5 Output Capacitor
- 9.2.2.6 Current Sensing Network
- 9.2.2.7 Gate Drive Resistor
- 9.2.2.8 VREF Capacitor
- 9.2.2.9 RT/CT
- 9.2.2.10 Start-Up Circuit
- 9.2.2.11 Voltage Feedback Compensation
- 9.2.3 Application Curves
- 9.2.4 Power Supply Recommendations
- 9.2.5 Layout
- 10Device and Documentation Support
- 11Mechanical, Packaging, and Orderable Information
Package Options
Mechanical Data (Package|Pins)
- D|8
Thermal pad, mechanical data (Package|Pins)
Orderable Information
9.2.2.11.2 Slope Compensation
Slope compensation is the large signal subharmonic instability that can occur with duty cycles that may extend beyond 50% where the rising primary side inductor current slope may not match the falling secondary side current slope. The subharmonic oscillation would result in an increase in the output voltage ripple and may even limit the power handling capability of the converter.
The target of slope compensation is to achieve an ideal quality coefficient (QP), equal to 1 at half of the switching frequency. The QP is calculated with Equation 31.
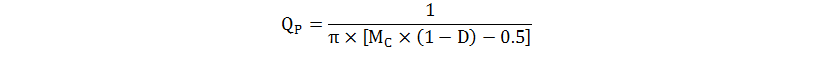
where
- D is the primary side switch duty cycle
- MC is the slope compensation factor, which is defined with Equation 32
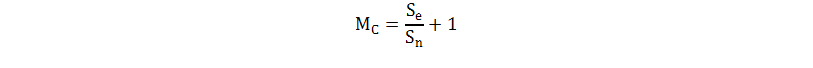
where
- Se is the compensation ramp slope
- Sn is the inductor rising slope
The optimal goal of the slope compensation is to achieve QP = 1; upon rearranging Equation 32 the ideal value of slope compensation factor is determined:
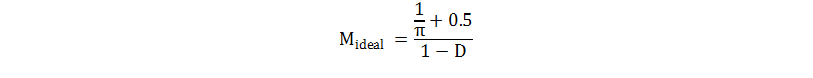
For this design to have adequate slope compensation, MC must be 2.193 when D reaches it maximum value of 0.627.
The inductor rising slope (Sn) at the CS pin is calculated with Equation 34.
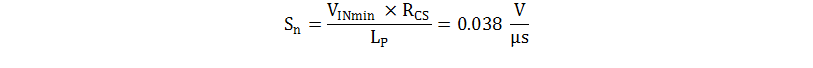
The compensation slope (Se) is calculated with Equation 35.
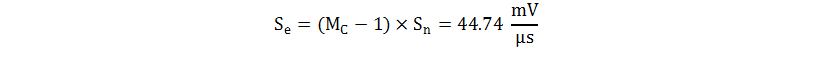
The compensation slope is added into the system through RRAMP and RCSF. The CRAMP is an AC-coupling capacitor that allows the voltage ramp of the oscillator to be used without adding an offset to the current sense; select a value to approximate a high-frequency short circuit, such as 10 nF, as a starting point and make adjustments if required. The RRAMP and RCSF resistors form a voltage divider from the oscillator charge slope and this proportional ramp is injected into the CS pin to add slope compensation. Choose the value of RRAMP to be much larger than the RRT resistor so that it does not load down the internal oscillator and result in a frequency shift. The oscillator charge slope is calculated using the peak-to-peak voltage of the RT/CT sawtooth waveform (VOSCpp) equal to 1.9 V, and the minimum ON time, as shown in Equation 37.
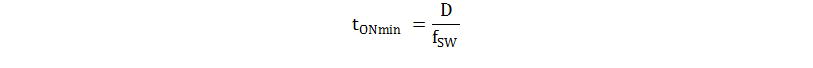
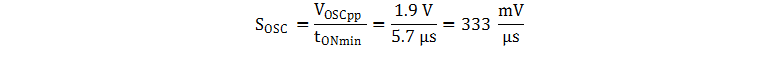
To achieve a 44.74-mV/µs compensation slope, RCSF is calculated with Equation 38. In this design, RRAMP is selected as 24.9 kΩ, a 3.8-kΩ resistor was selected for RCSF.
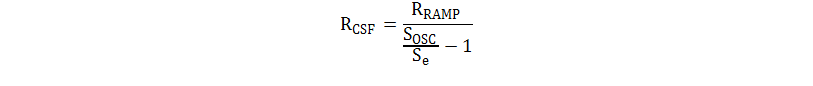
It has to be noticed that due to the PN junction of the BJT transistor, it can only source current, which means the capacitor CRAMP can only be charged, not discharged. Therefore, an extra discharge resistor RDIS is needed. Choose RDIS to be 1/10 of the RRAMP.